1. Линейность:  ;
;
2. Аддитивность:  ;
;
3. При изменении ориентации поверхности, поверхностный интеграл меняет знак.
20 Вычисление поверхностного интеграла
Вычисление поверхностного интеграла второго рода. Пусть поверхность  взаимно однозначно проецируется в область
взаимно однозначно проецируется в область  на плоскости Оху. В этом случае
на плоскости Оху. В этом случае  имеет одинаковый знак во всех точках поверхности. Именно,
имеет одинаковый знак во всех точках поверхности. Именно,  , если рассматривается верхняя сторона поверхности, и
, если рассматривается верхняя сторона поверхности, и  , если рассматривается нижняя сторона. Поэтому для верхней стороны все слагаемые в интегральной сумме должны браться со знаком "+", и сумма будет иметь вид
, если рассматривается нижняя сторона. Поэтому для верхней стороны все слагаемые в интегральной сумме должны браться со знаком "+", и сумма будет иметь вид  . Если поверхность задана уравнением
. Если поверхность задана уравнением  ,
, 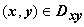 , то эта сумма равна
, то эта сумма равна  . В последней сумме легко увидеть интегральную сумму для двойного интеграла
. В последней сумме легко увидеть интегральную сумму для двойного интеграла  . Переход к пределу при
. Переход к пределу при  (при этом и
(при этом и  ) даст
) даст
 . Напомню, что эта формула получена для верхней стороны поверхности. Если выбрана нижняя сторона, то все слагаемые в интегральной сумме должны браться со знаком "-", и интегральная сумма будет иметь вид
. Напомню, что эта формула получена для верхней стороны поверхности. Если выбрана нижняя сторона, то все слагаемые в интегральной сумме должны браться со знаком "-", и интегральная сумма будет иметь вид  . Рассуждая, как и для верхней стороны, получим, что в этом случае
. Рассуждая, как и для верхней стороны, получим, что в этом случае  . Окончательно,
. Окончательно,  , где знак "+" берётся для верхней стороны поверхности, знак "-" - для нижней стороны.
, где знак "+" берётся для верхней стороны поверхности, знак "-" - для нижней стороны.
Аналогично изложенному, для других интегралов:  , если поверхность однозначно проецируется в область
, если поверхность однозначно проецируется в область  на плоскости Oyz, при этом знак "+" берётся для "передней" стороны поверхности (где
на плоскости Oyz, при этом знак "+" берётся для "передней" стороны поверхности (где  ), для "задней" стороны, где
), для "задней" стороны, где  , берётся знак "-";
, берётся знак "-";  , если поверхность однозначно проецируется в область
, если поверхность однозначно проецируется в область  на плоскость Oхz, знак "+" берётся для "правой" стороны поверхности (где
на плоскость Oхz, знак "+" берётся для "правой" стороны поверхности (где  ), для "левой" стороны, где
), для "левой" стороны, где  , берётся знак "-". Как и для поверхностного интеграла первого рода, если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
, берётся знак "-". Как и для поверхностного интеграла первого рода, если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
 Примеры. 1. Вычислить
Примеры. 1. Вычислить  , s - часть поверхности цилиндра y =
, s - часть поверхности цилиндра y =  , заключенная между плоскостями x=0, x=8, z=0, z=3. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oх.
, заключенная между плоскостями x=0, x=8, z=0, z=3. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oх.
Решение: Определяем знаки направляющих косинусов нормали cosa>0, cosb<0, cosg=0. Поэтому

 , где
, где
Dyz={(y,z): 0£ y £16, 0 £ z £ 3}, Dxz={(x,z): 0 £ x £ 8, 0 £ z £ 3} - проекции s на плоскости Oyz и Oxz соответственно. Проекция поверхности sна плоскость Oxy вырождается в линию - параболу y=  , cosg=0, поэтому интеграл по Dxy в данном случае отсутствует. Вычислим отдельно интегралы по Dyz и Dxz, выражая x(y,z) и y(x,z) из уравнения поверхности s: x(y,z)=2
, cosg=0, поэтому интеграл по Dxy в данном случае отсутствует. Вычислим отдельно интегралы по Dyz и Dxz, выражая x(y,z) и y(x,z) из уравнения поверхности s: x(y,z)=2  , y(x,z)=
, y(x,z)=  .
.
 =
=  =
=  dy=328,
dy=328, 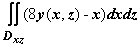 =
=  =
=  dx=928. Окончательно I = 328 - 928 = - 600.
dx=928. Окончательно I = 328 - 928 = - 600.
2. Вычислить  , где s - часть плоскости
, где s - часть плоскости  , ограниченная координатными плоскостями x=0, у=0, z=0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz.
, ограниченная координатными плоскостями x=0, у=0, z=0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz.
Решение. Из двух направлений нормали к s  мы должны выбрать такое, для которого коэффициент при орте
мы должны выбрать такое, для которого коэффициент при орте  (т.е.
(т.е.  ) положителен, поэтому выбираем знак "-", тогда
) положителен, поэтому выбираем знак "-", тогда  . В соответствии со знаками направляющих косинусов,
. В соответствии со знаками направляющих косинусов, 
 . Вычисляем эти интегралы.
. Вычисляем эти интегралы.


 .
.

 .
.

 . Окончательно,
. Окончательно, 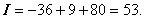
В заключение напомню, что вычисление поверхностного интеграла второго рода всегда можно свести к вычислению поверхностного интеграла первого рода. Так, в последнем примере подынтегральное выражение равно  , где
, где  ,
, 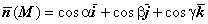
 . Поэтому
. Поэтому  , и, проектируя s на плоскость Оху
, и, проектируя s на плоскость Оху  , получим
, получим 
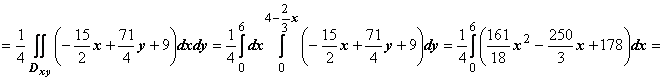
 .
.
24 Однородные уравнения первого порядка.
Определение однородного дифференциального уравнения
Дифференциальное уравнение первого порядка
 называется однородным, если правая часть удовлетворяет соотношению
называется однородным, если правая часть удовлетворяет соотношению
 для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
 Однородное дифференциальное уравнение можно также записать в виде
Однородное дифференциальное уравнение можно также записать в виде
 или через дифференциалы:
или через дифференциалы:
 где P (x,y) и Q (x,y) − однородные функции одинакового порядка.
Определение однородной функции
Функция P (x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:
где P (x,y) и Q (x,y) − однородные функции одинакового порядка.
Определение однородной функции
Функция P (x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:
 Решение однородных дифференциальных уравнений
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными. Дифференциальное уравнение вида
Решение однородных дифференциальных уравнений
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными. Дифференциальное уравнение вида
 преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:
преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:

|
| Пример 1
|
| |
Решить дифференциальное уравнение  .
Решение.
Нетрудно заметить, что многочлены P (x,y) и Q (x,y), соответственно, при dx и dy, являются однородными функциями первого порядка. Поэтому, данное дифференциальное уравнение также будет однородным. Положим y = ux, где u − некоторая новая функция, зависящая от x. Тогда .
Решение.
Нетрудно заметить, что многочлены P (x,y) и Q (x,y), соответственно, при dx и dy, являются однородными функциями первого порядка. Поэтому, данное дифференциальное уравнение также будет однородным. Положим y = ux, где u − некоторая новая функция, зависящая от x. Тогда
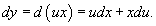 Подставляя это в дифференциальное уравнение, получаем
Подставляя это в дифференциальное уравнение, получаем
 Следовательно,
Следовательно,
 Разделим обе части уравнения на x:
Разделим обе части уравнения на x:
 Выполняя деление x, мы могли потерять решение x = 0. Прямая подстановка показывает, что x = 0действительно является одним из решений нашего уравнения. Интегрируем последнее выражение:
Выполняя деление x, мы могли потерять решение x = 0. Прямая подстановка показывает, что x = 0действительно является одним из решений нашего уравнения. Интегрируем последнее выражение:
 где C − постоянная интегрирования. Возвращаясь к старой переменной y, можно записать:
где C − постоянная интегрирования. Возвращаясь к старой переменной y, можно записать:
 Таким образом, уравнение имеет два решения:
Таким образом, уравнение имеет два решения:

|
26 Некоторые уравнения, допускающие понижение порядка

 ;
; ;
; взаимно однозначно проецируется в область
взаимно однозначно проецируется в область  на плоскости Оху. В этом случае
на плоскости Оху. В этом случае  имеет одинаковый знак во всех точках поверхности. Именно,
имеет одинаковый знак во всех точках поверхности. Именно,  , если рассматривается верхняя сторона поверхности, и
, если рассматривается верхняя сторона поверхности, и  , если рассматривается нижняя сторона. Поэтому для верхней стороны все слагаемые в интегральной сумме должны браться со знаком "+", и сумма будет иметь вид
, если рассматривается нижняя сторона. Поэтому для верхней стороны все слагаемые в интегральной сумме должны браться со знаком "+", и сумма будет иметь вид  . Если поверхность задана уравнением
. Если поверхность задана уравнением  ,
, 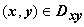 , то эта сумма равна
, то эта сумма равна  . В последней сумме легко увидеть интегральную сумму для двойного интеграла
. В последней сумме легко увидеть интегральную сумму для двойного интеграла  . Переход к пределу при
. Переход к пределу при  (при этом и
(при этом и  ) даст
) даст . Напомню, что эта формула получена для верхней стороны поверхности. Если выбрана нижняя сторона, то все слагаемые в интегральной сумме должны браться со знаком "-", и интегральная сумма будет иметь вид
. Напомню, что эта формула получена для верхней стороны поверхности. Если выбрана нижняя сторона, то все слагаемые в интегральной сумме должны браться со знаком "-", и интегральная сумма будет иметь вид  . Рассуждая, как и для верхней стороны, получим, что в этом случае
. Рассуждая, как и для верхней стороны, получим, что в этом случае  . Окончательно,
. Окончательно,  , где знак "+" берётся для верхней стороны поверхности, знак "-" - для нижней стороны.
, где знак "+" берётся для верхней стороны поверхности, знак "-" - для нижней стороны. , если поверхность однозначно проецируется в область
, если поверхность однозначно проецируется в область  на плоскости Oyz, при этом знак "+" берётся для "передней" стороны поверхности (где
на плоскости Oyz, при этом знак "+" берётся для "передней" стороны поверхности (где  ), для "задней" стороны, где
), для "задней" стороны, где  , берётся знак "-";
, берётся знак "-";  , если поверхность однозначно проецируется в область
, если поверхность однозначно проецируется в область  на плоскость Oхz, знак "+" берётся для "правой" стороны поверхности (где
на плоскость Oхz, знак "+" берётся для "правой" стороны поверхности (где  ), для "левой" стороны, где
), для "левой" стороны, где  , берётся знак "-". Как и для поверхностного интеграла первого рода, если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
, берётся знак "-". Как и для поверхностного интеграла первого рода, если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно. Примеры. 1. Вычислить
Примеры. 1. Вычислить  , s - часть поверхности цилиндра y =
, s - часть поверхности цилиндра y =  , заключенная между плоскостями x=0, x=8, z=0, z=3. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oх.
, заключенная между плоскостями x=0, x=8, z=0, z=3. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oх.
 , где
, где , cosg=0, поэтому интеграл по Dxy в данном случае отсутствует. Вычислим отдельно интегралы по Dyz и Dxz, выражая x(y,z) и y(x,z) из уравнения поверхности s: x(y,z)=2
, cosg=0, поэтому интеграл по Dxy в данном случае отсутствует. Вычислим отдельно интегралы по Dyz и Dxz, выражая x(y,z) и y(x,z) из уравнения поверхности s: x(y,z)=2  , y(x,z)=
, y(x,z)=  =
=  =
=  dy=328,
dy=328, 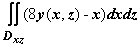 =
=  =
=  dx=928. Окончательно I = 328 - 928 = - 600.
dx=928. Окончательно I = 328 - 928 = - 600. , где s - часть плоскости
, где s - часть плоскости  , ограниченная координатными плоскостями x=0, у=0, z=0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz.
, ограниченная координатными плоскостями x=0, у=0, z=0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz. мы должны выбрать такое, для которого коэффициент при орте
мы должны выбрать такое, для которого коэффициент при орте  (т.е.
(т.е.  . В соответствии со знаками направляющих косинусов,
. В соответствии со знаками направляющих косинусов, 
 . Вычисляем эти интегралы.
. Вычисляем эти интегралы.

 .
.
 .
.
 . Окончательно,
. Окончательно, 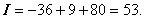
 , где
, где  ,
, 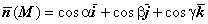
 . Поэтому
. Поэтому  , и, проектируя s на плоскость Оху
, и, проектируя s на плоскость Оху  , получим
, получим 
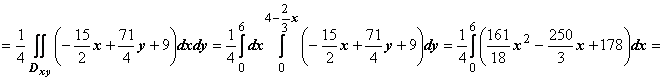
 .
. называется однородным, если правая часть удовлетворяет соотношению
называется однородным, если правая часть удовлетворяет соотношению
 для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
 Однородное дифференциальное уравнение можно также записать в виде
Однородное дифференциальное уравнение можно также записать в виде
 или через дифференциалы:
или через дифференциалы:
 где P (x,y) и Q (x,y) − однородные функции одинакового порядка.
Определение однородной функции
Функция P (x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:
где P (x,y) и Q (x,y) − однородные функции одинакового порядка.
Определение однородной функции
Функция P (x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:
 Решение однородных дифференциальных уравнений
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными. Дифференциальное уравнение вида
Решение однородных дифференциальных уравнений
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными. Дифференциальное уравнение вида
 преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:
преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:

 .
Решение.
Нетрудно заметить, что многочлены P (x,y) и Q (x,y), соответственно, при dx и dy, являются однородными функциями первого порядка. Поэтому, данное дифференциальное уравнение также будет однородным. Положим y = ux, где u − некоторая новая функция, зависящая от x. Тогда
.
Решение.
Нетрудно заметить, что многочлены P (x,y) и Q (x,y), соответственно, при dx и dy, являются однородными функциями первого порядка. Поэтому, данное дифференциальное уравнение также будет однородным. Положим y = ux, где u − некоторая новая функция, зависящая от x. Тогда
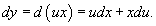 Подставляя это в дифференциальное уравнение, получаем
Подставляя это в дифференциальное уравнение, получаем
 Следовательно,
Следовательно,
 Разделим обе части уравнения на x:
Разделим обе части уравнения на x:
 Выполняя деление x, мы могли потерять решение x = 0. Прямая подстановка показывает, что x = 0действительно является одним из решений нашего уравнения. Интегрируем последнее выражение:
Выполняя деление x, мы могли потерять решение x = 0. Прямая подстановка показывает, что x = 0действительно является одним из решений нашего уравнения. Интегрируем последнее выражение:
 где C − постоянная интегрирования. Возвращаясь к старой переменной y, можно записать:
где C − постоянная интегрирования. Возвращаясь к старой переменной y, можно записать:
 Таким образом, уравнение имеет два решения:
Таким образом, уравнение имеет два решения:




