y (x) = С1 y 1 (х) + С 2 y 2 (х) +... + Сnyn (х), (9)
где Сi (i = 1, 2,..., n) -произвольные константы.
Таким образом, теорема 5 фактически утверждает, что пространство решений данного линейного однородного уравнения n -го порядка имеет базис - ФСР, который состоит из n решений.
П р и м е р 5. Показать, что функции у 1(х) = sinх, у 2(х) = cosх образуют фундаментальную систему решений уравнения у¢¢ (х) + у (х) = 0. Записать общее решение уравнения.
Решение. Очевидно, что функции у 1(х) = sinх, у 2(х) = cosх удовлетворяют данному уравнению. По теореме 3 они линейно независимы на всей числовой оси, так как W [ sinx, cosx ] º -1 (см. пример 3). Таким образом, они являются фундаментальной системой решений. Общим решением является функция у (х) = С 1 sinx + C 2 cosx (cм. теорему 5).
28 Определитель Вронского и его свойства
Вронскиа́н (определитель Вронского) системы функций 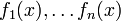 , дифференцируемых на промежутке
, дифференцируемых на промежутке 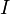 (n-1)-раз — функция на
(n-1)-раз — функция на 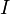 , задаваемая определителем следующейматрицы:
, задаваемая определителем следующейматрицы:
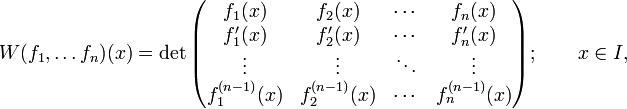 .
.
Также вронскианом называют функцию, заданную определителем более общего вида. А именно, пусть задано n вектор-функций  с n компонентами:
с n компонентами: 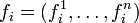 . Тогда определитель будет выглядеть так (чтобы избежать разночтений обозначим его
. Тогда определитель будет выглядеть так (чтобы избежать разночтений обозначим его 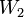 ):
):
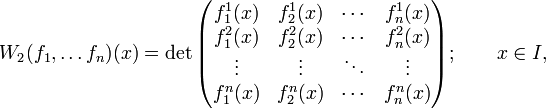 .
.
Определитель Вронского применяется для решения дифференциальных уравнений, например для того, чтобы узнать, являются ли найденные решения однородного линейного дифференциального уравнения (либо системы уравнений) линейно независимыми. Это помогает в поиске его общего решения.
Свойства
§ Если  — линейно зависимы на
— линейно зависимы на 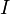 , то
, то 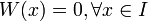 .
.
§ Если определитель Вронского на интервале отличается от нуля хотя бы в одной точке, то функции  являются линейно независимыми (прямое следствие предыдущего свойства). Обратное вообще говоря неверно (см. пример 3), но для случая, когда функции являются решениями дифференциального уравнения будут верны более сильные следствия (см. ниже).
являются линейно независимыми (прямое следствие предыдущего свойства). Обратное вообще говоря неверно (см. пример 3), но для случая, когда функции являются решениями дифференциального уравнения будут верны более сильные следствия (см. ниже).
§ Если  - решения линейного однородного дифференциального уравнения
- решения линейного однородного дифференциального уравнения 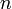 -го порядка, то
-го порядка, то 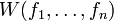 называется вронскианом этого уравнения. Определитель Вронского однородного дифференциального уравнения либо тождественно равен нулю, и это означает, что
называется вронскианом этого уравнения. Определитель Вронского однородного дифференциального уравнения либо тождественно равен нулю, и это означает, что  линейно зависимы, либо не обращается в нуль ни в одной точке
линейно зависимы, либо не обращается в нуль ни в одной точке 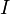 , что означает линейную независимость функций
, что означает линейную независимость функций  .
.
§ Если  - решения линейной однородной системы, то
- решения линейной однородной системы, то 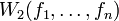 либо тождественно равен нулю, и это означает, что
либо тождественно равен нулю, и это означает, что  линейно зависимы, либо не обращается в нуль ни в одной точке
линейно зависимы, либо не обращается в нуль ни в одной точке 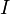 , что означает линейную независимость функций
, что означает линейную независимость функций  .
.
§ 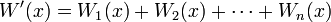 - где
- где 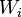 — определитель Вронского, в котором строка с номером i заменена строкой производных:
— определитель Вронского, в котором строка с номером i заменена строкой производных:
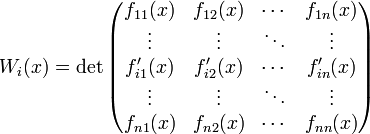
[править]Примеры
§ Убедимся, что вронскиан линейно-зависимых функций 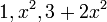 равен нулю:
равен нулю:
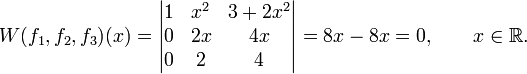
§ Проверим теперь линейную независимость функций 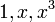
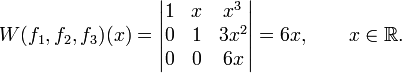
Есть точки, где вронскиан отличен от нуля (в нашем случае это любая точка, кроме x=0). Поэтому на любом промежутке эти функции будут линейно независимыми.
§ Приведём теперь пример, когда вронскиан всюду равен нулю, но функции всё равно линейно независимы. Зададим две функции:
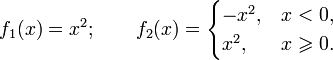
Обе функции всюду дифференцируемы (в том числе в нуле, где производные обеих функций обращаются в ноль). Убедимся, что вронскиан всюду ноль.
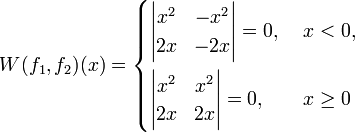
Однако эти функции, очевидно, являются линейно независимыми. Видим что равенство вронскиана нулю не влечёт за собой линейной зависимости в случае произвольного выбора функций.
32 Неоднородные линейные уравнения второго порядка с правой частью специального вида.
Линейное неоднородное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами имеет вид 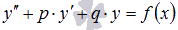 , где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X.
, где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X.
Сформулируем теорему, которая показывает в каком виде искать общее решение ЛНДУ.
Общее решение на интервале X линейного неоднородного дифференциального уравнения 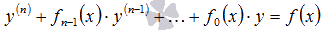 с непрерывными на интервале интегрирования X коэффициентами
с непрерывными на интервале интегрирования X коэффициентами  и непрерывной функцией f(x) равно сумме общего решения
и непрерывной функцией f(x) равно сумме общего решения  соответствующего ЛОДУ и какого-нибудь частного решения
соответствующего ЛОДУ и какого-нибудь частного решения 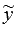 исходного неоднородного уравнения. То есть,
исходного неоднородного уравнения. То есть,  .
.
Таким образом, общим решением линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами является сумма  . Нахождение
. Нахождение  описано в статье линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами и нам осталось научиться определять
описано в статье линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами и нам осталось научиться определять 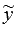 .
.
Существует несколько методов нахождения частного решения ЛНДУ второго порядка с постоянными коэффициентами. Методы выбираются в зависимости от вида функции f(x), стоящей с правой части уравнения. Перечислим их.
- Если f(x) является многочленом n-ой степени f(x) = Pn(x), то частное решение ЛНДУ ищется в виде
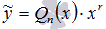 , где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как
, где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как 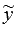 - частное решение уравнения
- частное решение уравнения 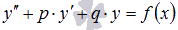 , то коэффициенты, определяющие многочлен Qn(x), находятся методом неопределенных коэффициентов из равенства
, то коэффициенты, определяющие многочлен Qn(x), находятся методом неопределенных коэффициентов из равенства 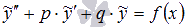 .
.
Перейти к решению примера...
- Если функция f(x) представлена произведением многочлена степени n и экспоненты
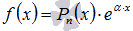 , то частное решение ЛНДУ второго порядка ищется в виде
, то частное решение ЛНДУ второго порядка ищется в виде 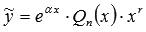 , где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных
, где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных 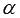 . Коэффициенты многочлена Qn(x) определяются из равенства
. Коэффициенты многочлена Qn(x) определяются из равенства 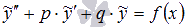 .
.
Перейти к решению примера...
- Если функция f(x) имеет вид
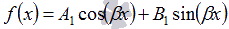 , где А1 и В1 – числа, то частное решение ЛНДУ представляется как
, где А1 и В1 – числа, то частное решение ЛНДУ представляется как 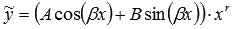 , где А и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных
, где А и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных 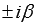 . Коэффициенты многочлена А и В находятся из равенства
. Коэффициенты многочлена А и В находятся из равенства 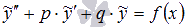 .
.
Перейти к решению примера...
- Если
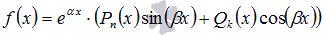 , то
, то 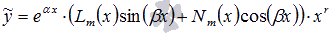 , где r – число комплексно сопряженных пар корней характеристического уравнения, равных
, где r – число комплексно сопряженных пар корней характеристического уравнения, равных 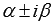 , Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства
, Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства 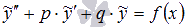 .
.
Перейти к решению примера...
- Для любого другого вида функции f(x) применяется следующий алгоритм действий.
Находится общее решение соответствующего линейного однородного уравнения как
y0 = C1 ⋅ y1 + C2 ⋅ y2, где y1 и y2 - линейно независимые частные решения ЛОДУ, а С1 и С2 – произвольные постоянные. Далее варьируются произвольные постоянные, то есть, в качестве общего решения исходного ЛНДУ принимается y = C1(x) ⋅ y1 + C2(x) ⋅ y2. Производные функций C1(x) и С2(x) определяются из системы уравнений 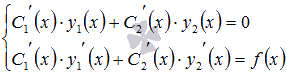 , а сами функции C1(x) и C2(x) находятся при последующем интегрировании.
, а сами функции C1(x) и C2(x) находятся при последующем интегрировании.
Перейти к решению примера...
Пример.
Решите задачу Коши  ,
,  .
.

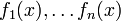 , дифференцируемых на промежутке
, дифференцируемых на промежутке 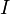 (n-1)-раз — функция на
(n-1)-раз — функция на 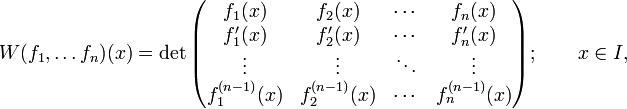 .
. с n компонентами:
с n компонентами: 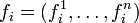 . Тогда определитель будет выглядеть так (чтобы избежать разночтений обозначим его
. Тогда определитель будет выглядеть так (чтобы избежать разночтений обозначим его  ):
):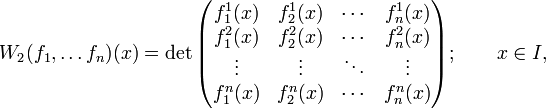 .
.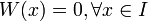 .
.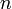 -го порядка, то
-го порядка, то 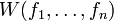 называется вронскианом этого уравнения. Определитель Вронского однородного дифференциального уравнения либо тождественно равен нулю, и это означает, что
называется вронскианом этого уравнения. Определитель Вронского однородного дифференциального уравнения либо тождественно равен нулю, и это означает, что 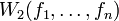 либо тождественно равен нулю, и это означает, что
либо тождественно равен нулю, и это означает, что 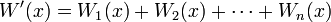 - где
- где 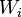 — определитель Вронского, в котором строка с номером i заменена строкой производных:
— определитель Вронского, в котором строка с номером i заменена строкой производных: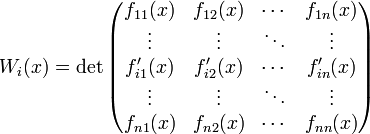
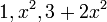 равен нулю:
равен нулю: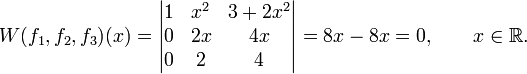
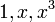
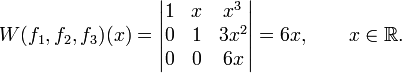
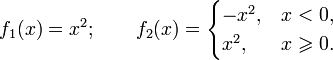

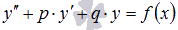 , где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X.
, где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X.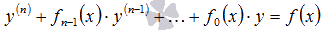 с непрерывными на интервале интегрирования X коэффициентами
с непрерывными на интервале интегрирования X коэффициентами  и непрерывной функцией f(x) равно сумме общего решения
и непрерывной функцией f(x) равно сумме общего решения  соответствующего ЛОДУ и какого-нибудь частного решения
соответствующего ЛОДУ и какого-нибудь частного решения 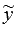 исходного неоднородного уравнения. То есть,
исходного неоднородного уравнения. То есть,  .
.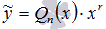 , где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как
, где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как 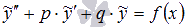 .
.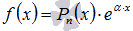 , то частное решение ЛНДУ второго порядка ищется в виде
, то частное решение ЛНДУ второго порядка ищется в виде 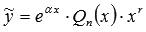 , где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных
, где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных 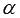 . Коэффициенты многочлена Qn(x) определяются из равенства
. Коэффициенты многочлена Qn(x) определяются из равенства 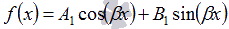 , где А1 и В1 – числа, то частное решение ЛНДУ представляется как
, где А1 и В1 – числа, то частное решение ЛНДУ представляется как 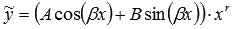 , где А и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных
, где А и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных 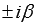 . Коэффициенты многочлена А и В находятся из равенства
. Коэффициенты многочлена А и В находятся из равенства 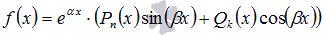 , то
, то 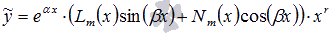 , где r – число комплексно сопряженных пар корней характеристического уравнения, равных
, где r – число комплексно сопряженных пар корней характеристического уравнения, равных 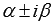 , Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства
, Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства 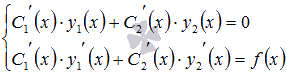 , а сами функции C1(x) и C2(x) находятся при последующем интегрировании.
, а сами функции C1(x) и C2(x) находятся при последующем интегрировании. ,
,  .
.


