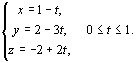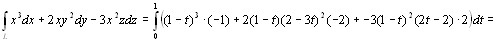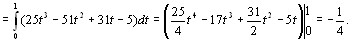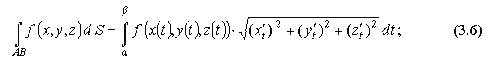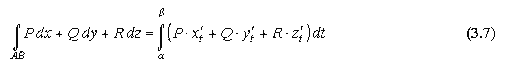Криволинейные интегралы первого и второго рода, их свойства и вычисление.
Рассмотрим на плоскости или в пространстве кривую L и функцию f, определенную в каждой точке этой кривой. Разобьем кривую на части Δsi длиной Δsi и выберем на каждой из частей точку Mi. Составим интегральную сумму Определение 10.1. Если существует конечный предел интегральной суммы
Например, если функция f(M) задает плотность в точке М, то интеграл (10.1) равен массе рассматриваемой кривой.
Свойства криволинейного интеграла 1-го рода.
1. Если функция f непрерывна на кривой L, то интеграл 2. Криволинейный интеграл 1-го рода не зависит от направления движения по кривой, то есть от того, какую из точек, ограничивающих кривую, считать начальной, а какую – конечной. Если назвать эти точки А и В, то
Справедливость этих свойств следует из определения криволинейного интеграла 1-го рода.
Способ вычисления криволинейного интеграла 1-го рода.
Выберем на кривой L направление от начальной точки А и отметим, что положение точки М на кривой определяется длиной дуги АМ = s. Тогда кривую L можно задать параметрически: x = x(s), y = y(s), z = z(s), где
где
Если же кривая L задана в параметрической форме: x = φ(t), y = ψ(t), z = χ(t), t0 ≤ t ≤ T, то, применяя в интеграле (10.3) формулу замены переменной и учитывая, что дифференциал дуги
получим:
Таким образом, вычисление криволинейного интеграла 1-го рода сводится к вычислению обычного определенного интеграла от функции переменной t в пределах, соответствующих изменению значения этой переменной на рассматриваемой кривой.
Пример. Вычислить
Криволинейный интеграл второго рода.
Вновь рассмотрим кривую L, в каждой точке которой задана функция f(M), и зададим разбиение кривой на отрезки. Выберем на каждом отрезке точку Mi и умножим значе-ние функции в этой точке не на длину i-го отрезка, как в случае криволинейного инте-грала 1-го рода, а на проекцию этого отрезка, скажем, на ось Ох, то есть на разность xi – xi-1 = Δxi. Составим из полученных произведений интегральную сумму Определение 10.2. Если существует конечный предел при
Подобным образом можно определить и криволинейные интегралы 2-го рода вида
Определение 10.3. Если вдоль кривой L определены функции P(M) = P(x, y, z), Q(M) = Q(x, y, z), R(M) = R(x, y, z) и существуют интегралы
то и их сумму называют криволинейным интегралом второго рода (общего вида) и полагают
Замечание. Если считать, что сила
то есть криволинейным интегралом 2-го рода.
Свойства криволинейного интеграла 2-го рода.
1. Если функции P(M), Q(M), R(M) непрерывны на кривой (АВ), то интеграл (10.6) существует (справедливость этого утверждения следует из определения 10.2).
1. При изменении направления кривой (то есть перемены местами начальной и конечной ее точек) криволинейный интеграл 2-го рода меняет знак:
Действительно, при этом изменяется знак Δxi в интегральной сумме.
Способ вычисления криволинейного интеграла 2-го рода.
Теорема 10.1. Пусть кривая L задана параметрическими уравнениями x = φ(t), y = ψ(t), z = χ(t), α ≤ t ≤ β, где φ, ψ, χ – непрерывно дифференцируемые функции, и на ней задана непрерывная функция f(x, y, z). Тогда интеграл (10.5) существует и имеет место равенство
Доказательство. Запишем Δxi = xi – xi-1 = φ(ti) – φ(ti-1) и преобразуем последнюю разность по формуле Лагранжа: φ(ti) – φ(ti-1) = φ΄(τi)Δti, где τi – некоторое значение t, заключенное между ti-1 и ti. Выберем точку Мi так, чтобы ее координаты соответствовали значению параметра, равному τi: Mi(φ(τi), ψ(τi), χ(τi)). Подставив эти значения в формулу (10.5), получим:
Справа получен предел интегральной суммы для функции f(φ(t),ψ(t),χ(t))φ΄(t) на отрезке [α, β], равный определенному интегралу от этой функции:
что и требовалось доказать.
Следствие. Аналогичные соотношения можно получить для криволинейных интегра-лов вида
Пример. Вычислим интеграл
Следовательно, φ΄(t) = -1, ψ΄(t) = -3, χ΄(t) = 2. Тогда
15 Вычисление криволинейного интеграла.
а) криволинейный интеграл 1-го рода:
б) криволинейный интеграл 2-го рода:
Пример 3.1. Найти массу четверти окружности x2+y2=R2, х≥0, у≥0, если плотность в каждой точке окружности равна ординате этой точки.
|

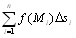 . Назовем λ длину наибольшего отрезка кривой.
. Назовем λ длину наибольшего отрезка кривой.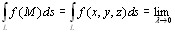
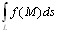 существует.
существует.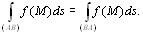 (10.2)
(10.2)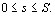 Функция f(x,y,z) становится при этом сложной функцией одной переменной s: f(x(s), y(s), z(s)). Тогда интегральная сумма
Функция f(x,y,z) становится при этом сложной функцией одной переменной s: f(x(s), y(s), z(s)). Тогда интегральная сумма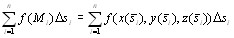 ,
,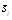 - координата точки Mi, является обычной интегральной суммой для определен-ного интеграла
- координата точки Mi, является обычной интегральной суммой для определен-ного интеграла 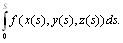 Следовательно,
Следовательно,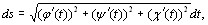
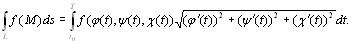 (10.4)
(10.4)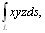 где L:
где L: 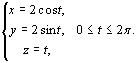 Применяя формулу (10.4), получим:
Применяя формулу (10.4), получим: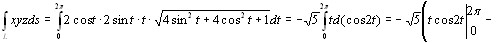
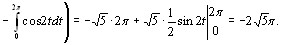
 .
.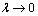 интегральной суммы
интегральной суммы 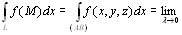
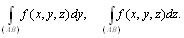
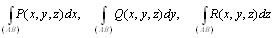 ,
,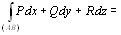
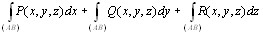 . (10.6)
. (10.6)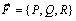 действует на точку, движущуюся по кривой (АВ), то работа этой силы может быть представлена как
действует на точку, движущуюся по кривой (АВ), то работа этой силы может быть представлена как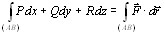 ,
,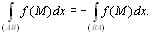 (10.7)
(10.7)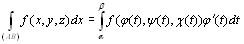 . (10.8)
. (10.8)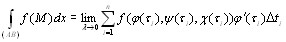 .
.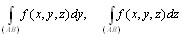 , откуда следует, что
, откуда следует, что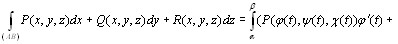
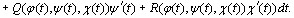 (10.9)
(10.9)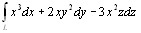 , где L – отрезок прямой от точки А(1,2,-2) до точки В(0, -1, 0). Запишем уравнение этой прямой в параметрическом виде:
, где L – отрезок прямой от точки А(1,2,-2) до точки В(0, -1, 0). Запишем уравнение этой прямой в параметрическом виде: