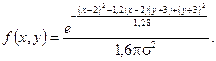Звичайні задачі. Задача № 1. Закон розподілу ймовірностей системи двох дискретних випадкових ве­ли­чин Х та Y, p(x, y)

Задача № 1. Закон розподілу ймовірностей системи двох дискретних випадкових ве­ли­чин Х та Y, p (x, y), заданий у нас­тупній таблиці.

X Y	-2	-1
	0,01	0,03	0,02	0,01	0,005	0,008
	0,01	0,02	0,08	0,2	0,1	0,005
	0,1	0,3	0,05	0,02	0,03	0,002

За наведеною таблицею визначити.

1. Закони розподілу одновимірних величин Х та Y, p (x) та p (y) відповідно. Побудувати графіки функ­цій розподілу цих величин F (x) та F (y).

2. Знайти ймовірність того, що величина Х є меншою, ніж Y, тобто P { X < Y }.

3. Знайти математичне сподівання, дисперсію та середнє квадратичне відхилення для ви­падкових величин Х та Y.

4. Обчислити кореляційний момент та коефіцієнт кореляції випадкових ве­ли­чин Х та Y.

Задача № 2. Двовимірна неперервна випадкова величина (X, Y) має закон розподілу:

Знайти ймовірність того, що випадкова величина (X, Y) знаходиться в інтервалі: Побудувати графік функції F (X, Y).

Задача № 3. Знайти кореляційний момент та коефіцієнт кореляції неперервної дво­ви­мірної випад­кової величи­ни (X, Y), якщо густина розподілу її ймовірності має вигляд:

Побудувати графік функції f (x, y).

Задача № 4. Пристрій, структурна схема якого наведена на рис. 1, складається із чоти­рьох блоків. Се­ред­ній час безвідмовної роботи першого блоку складає 150 годин, другого – 500 годин, третього – 300 годин, чет­вертого – 200 годин. Знайти ймовірність того, що прист­рій не вийде з ладу за 250 годин.

Задача № 5. Густина розподілу випадкових ве­ли­чин (Х, Y) задана формулою, яка відповідає нормальному розподілу:

Знайти математичне сподівання, дисперсію та середнє квадратичне відхилення для ви­падкових величин Х та Y, а також коефіцієнт кореляції.

Задача № 6. Побудувати графічні залежності для розподілів двовимірних випадкових величин із наступними параметрами.

1. Для гама-розподілу, α = [1, 2, 3, 4, 5, 6], β = [1, 2, 3].

2. Для χ² – розподілу, k = [1, 2, 3, 4, 5, 6].

3. Для двовимірного нормального розподілу, m ₁ = m ₂ = 0, σ₁ = 0,001, σ₂ = 0,005, r = 0,2. Знайти такі параметри нормального розподілу, для яких r = 0.