Задачі підвищеної складності. Задача № 1. Дві людини домовились між собою зустрітися біля входу до станції метро «Політехнічний інститут» у проміжку між сімнадцятою та вісімнадцятою

Задача № 1. Дві людини домовились між собою зустрітися біля входу до станції метро «Політехнічний інститут» у проміжку між сімнадцятою та вісімнадцятою годинами, але жо­ден з них не вказав точний час, коли він прийде. Проте вони домовились про те, що той, хто прийде раніше, буде чекати другого протягом 15 хвилин. Яка ймовірність того, що ці люди зуст­рі­нуть­ся?

Задача № 2. Урозглянутій на практичному занятті задачі №7 була отримана формула для ймо­вір­ності здачі студентом іспиту у разі, якщо кіль­кість питань, які задає викладач сту­дентові, k = 3. Отримати відповідні формули для кількості питань k = 4 та k = 5. Побудувати гра­фічні залеж­ності P (n) для k = 3, k = 4 та k = 5. Проаналізувати отримані графічні результати та зробити відповідні висновки.

Задача № 3. Урозглянутій на практичному занятті задачі №4 була отримана формула для ймовір­нос­ті очікування автобусу: , де t – час очікування, T ₁ – ін­тер­­вал, з яким ходить автобус першого маршруту, T ₂ – інтервал, з яким ходить автобус першого маршруту.

Побудувати графічні залежності P (t) для таких параметрів випадкового процесу:

а) T ₁ = 20 хв.; T ₂ = 10 хв., 12 хв., 15 хв., 18 хв. ;

б) T ₂ = 10 хв.; T ₁ = 15 хв., 20 хв., 25 хв., 30 хв. .

Проаналізувати отримані графічні результати та зробити відповідні висновки. Отримати також графічні залежності для випадків t > T ₁ та t > T ₂. Чи є такі випадки мож­­ливими і чому?

Задача № 4. На окружності навмання, випадковим чином, поставлені три крапки: A, B та C. Знайдіть ймо­вір­ність того, що трикутник ABC є гострокутним.

Задача № 5. Задача Бюффона.На площині проведені паралельні лінії, відстань між якими становить L. На цю площину навмання кидається голка розміром l (l < L). Знайти ймо­вірність того, що голка перетне будь-яку лінію.

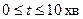Задача № 6. Дві частинки з радіусами r та R (r < R) рухаються у довільному нап­рямку із швидкостями та 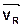. Знайдіть ймовірність зіткнення цих двох частинок.