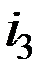На рис. 1.6а изображена схема идеальной емкости для мгновенных значений
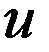
,
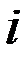
и соответствующая схема (рис. 1.6б) с символической записью.
 - комплексное емкостное сопротивление.
- комплексное емкостное сопротивление.
 величина реактивного емкостного сопротивления,
величина реактивного емкостного сопротивления,  .
.
Реактивное емкостное сопротивление 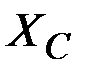 - отрицательное. В данном случае действие интегрирования для мгновенных значений заменяется действием деления на
- отрицательное. В данном случае действие интегрирования для мгновенных значений заменяется действием деления на  для изображающих векторов или комплексных чисел. На емкости сдвиг по фазе тока относительно напряжения
для изображающих векторов или комплексных чисел. На емкости сдвиг по фазе тока относительно напряжения  (рис. 1.6в).
(рис. 1.6в).
При постоянном токе  - разрыв,
- разрыв,  учитывает накопление энергии в электрическом поле конденсатора.
учитывает накопление энергии в электрическом поле конденсатора.
В символическом методе синусоидальная функция заменяется соответствующим комплексом, действие дифференцирования - умножением на  , действие интегрирования - делением на
, действие интегрирования - делением на  .
.

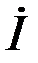
| сущность символического метода
|



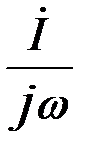
 - закон Ома в символической форме
- закон Ома в символической форме
Первый закон Кирхгофа
Геометрическая сумма изображающих векторов токов в узле равна нулю
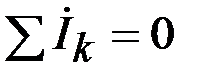
- первый закон Кирхгофа
На рис. 1.7а показан узел некоторой схемы и использованы обозначения мгновенных значений токов, на рис. 1.7б - соответствующая схема с символической записью.
Пример 1.
Определить в схеме рис. 1.8а показание амперметра тепловой системы, если: 
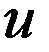 ,
, 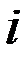 и соответствующая схема (рис. 1.6б) с символической записью.
и соответствующая схема (рис. 1.6б) с символической записью.


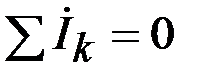 - первый закон Кирхгофа
- первый закон Кирхгофа


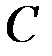








 - комплексное емкостное сопротивление.
- комплексное емкостное сопротивление. величина реактивного емкостного сопротивления,
величина реактивного емкостного сопротивления,  .
.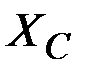 - отрицательное. В данном случае действие интегрирования для мгновенных значений заменяется действием деления на
- отрицательное. В данном случае действие интегрирования для мгновенных значений заменяется действием деления на  для изображающих векторов или комплексных чисел. На емкости сдвиг по фазе тока относительно напряжения
для изображающих векторов или комплексных чисел. На емкости сдвиг по фазе тока относительно напряжения  (рис. 1.6в).
(рис. 1.6в). - разрыв,
- разрыв,  учитывает накопление энергии в электрическом поле конденсатора.
учитывает накопление энергии в электрическом поле конденсатора. , действие интегрирования - делением на
, действие интегрирования - делением на  .
.
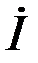

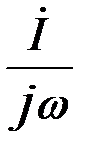
 - закон Ома в символической форме
- закон Ома в символической форме