Решение. В общем случае для цепи рис
В общем случае для цепи рис. 1.11а имеем с учетом второго закона Кирхгофа:
где
Ток 1)
Сдвиг по фазе тока относительно напряжения 2) Расчеты и построения векторной диаграммы аналогичны первому случаю, но 3) В этом случае
Это частный режим, когда
1.5. Применение комплексных чисел к Комплексное число может быть изображено на комплексной плоскости вектором, проведенным из начала координат (рис. 1.12), который характеризуется величиной и положением относительно оси
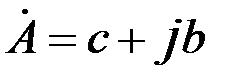 , тригонометрической - , тригонометрической - 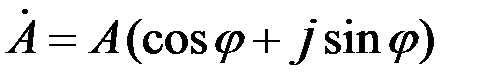 , показательной , показательной 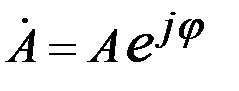 , где , где 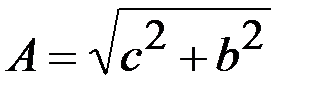 - модуль комплексного числа; - модуль комплексного числа; 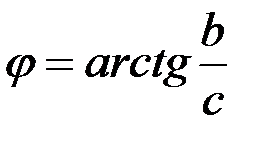 - аргумент комплексного числа. - аргумент комплексного числа.
Сложение и вычитание комплексных величин удобно производить в алгебраической форме, а умножение и деление - в показательной форме. В связи с этим надо часто переходить от одной формы комплексного числа к другой.
|

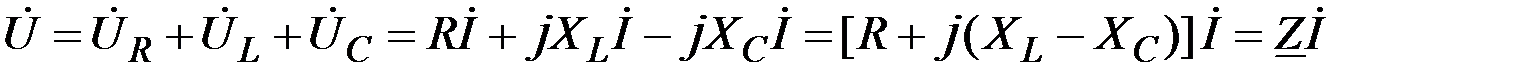 ,
, - комплексное сопротивление цепи;
- комплексное сопротивление цепи; - активное сопротивление;
- активное сопротивление;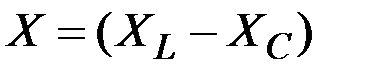 - реактивное сопротивление.
- реактивное сопротивление. - общий для последовательной цепи. Поэтому при построении векторной диаграммы для каждого случая сначала откладывается вектор тока
- общий для последовательной цепи. Поэтому при построении векторной диаграммы для каждого случая сначала откладывается вектор тока  . Рассмотрим каждый случай.
. Рассмотрим каждый случай. (рис. 1.11б)
(рис. 1.11б) - в фазе с током;
- в фазе с током; - вектор
- вектор  вращаем на
вращаем на  или на
или на  ;
; - вектор
- вектор  или на
или на  ;
; - направлен в сторону
- направлен в сторону 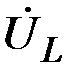 , т.к.
, т.к.  ;
;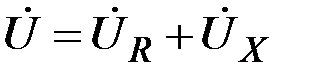 - по правилу параллелограмма.
- по правилу параллелограмма. откладываем от тока к напряжению.
откладываем от тока к напряжению. 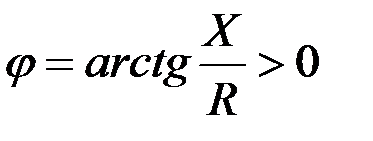 , т.к.
, т.к. 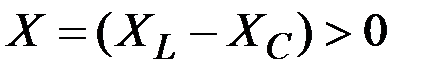
 (рис. 1.11г)
(рис. 1.11г) , поэтому
, поэтому  направлен в сторону
направлен в сторону  , и фазовый сдвиг
, и фазовый сдвиг  т.к.
т.к.  .
. (рис. 1.11в)
(рис. 1.11в) , но они в противофазе, поэтому
, но они в противофазе, поэтому ;
;  ;
;  , т.к.
, т.к.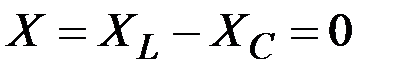
 , фазовый сдвиг
, фазовый сдвиг  , называемый резонансом напряжений.
, называемый резонансом напряжений. .
.








