К выполнению контрольной работы
Методические указания К выполнению контрольной работы
Братск 2013
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Братский государственный университет»
Электротехника и электроника
Расчет линейных электрических цепей синусоидального тока Методические указания к выполнению контрольной работы
Братск Издательство Братского государственного университета
УДК 621.313 Н.А.Астапенко. Электротехника и электроника. Расчет линейных электрических цепей синусоидального тока: методические указания к выполнению контрольной работы.- Братск: Изд-во БрГУ, 2013. - …….с.
Содержит краткие теоретические сведения, упражнения, типовое решение контрольной работы по дисциплине «Электротехника и электроника» для обучающихся по направлению подготовки бакалавров 190600 Эксплуатация транспортно-технологических машин и комплексов. Содержит 50 вариантов заданий, список литературы Рекомендовано обучающимся очной и заочной формы обучения.
Рецензент: Г.А.Большанин, канд. техн. наук, профессор кафедры ЭиЭ (ФГОУ ВПО «БрГУ»,г.Братск) Введение В соответствии с рекомендациями программы дисциплины «Общая электротехника и электроника» и действующему Федеральному государственному образовательному стандарту высшего профессионального образования, обучающиеся по направлению подготовки 190600 Эксплуатация транспортно-технологических машин и комплексов, где предусмотрена данная дисциплина, должны выполнить контрольную работу по теме «Расчет линейных цепей синусоидального тока». Самостоятельная работа над заданием включает предварительную проработку необходимого теоретического материала [1, 3, 6]. С целью облегчения усвоения необходимого теоретического материала методическое пособие содержит краткие теоретические сведения, несложные примеры, позволяющие закрепить теоретические знания и типовое решение контрольной работы.
1. Электрические цепи однофазного 1.1. Переменные токи Переменным током называется ток, изменяющийся во времени по величине и направлению. Значение тока в любой данный момент времени называется мгновенным значением тока Токи, значения которых повторяются через равные промежутки времени в той же самой последовательности, называются периодическими. Наименьший промежуток времени, через который эти повторения наблюдаются, называется периодом Рассмотрим график некоторого периодического тока
 за период за период  охватывает один полный цикл изменения тока. Величина, обратная периоду охватывает один полный цикл изменения тока. Величина, обратная периоду  , называется частотой , называется частотой  , т.е. , т.е.
Максимальное значение функции
На рис.1.1б показана отдельная ветвь сложной схемы, т.е. двухполюсник ab. Стрелка на схеме указывает положительное направление тока
Все определения, данные здесь и ниже для тока, применимы для напряжений, ЭДС, магнитных потоков и любых других величин, изменяющихся во времени. В электроэнергетике и электротехнике наибольшее применение получили простые гармонические колебания или синусоидальные токи.
Синусоида представляет вертикальную проекцию вращающегося со скоростью
 - угловая частота, - угловая частота, 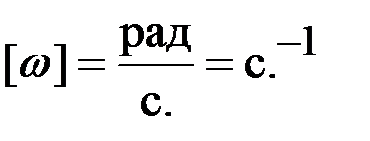
Для напряжения и ЭДС аналогично:
1.2. Среднее и действующее значения Под средним значением синусоидально изменяющейся величины понимают среднее ее значение за полпериода. Среднее значение синусоидального тока:
Аналогично получим среднее значение напряжения и ЭДС:
Среднее значение тока служит для сравнения постоянного и переменного тока по их электролитическому действию. Тепловое действие тока пропорционально квадрату тока. Поэтому для суждения о величине периодического тока вводят понятие о среднем квадратичном значении тока за период, которое называют действующим значением переменного тока. Действующее значение синусоидального тока:
Аналогично получим действующие значения напряжения и ЭДС:
Действующее значение переменного тока численно равно такому постоянному току, который за один период выделяет в сопротивлении такое же количество тепла, как и ток переменный. Отсюда и одинаковое их обозначение. Действующие значения измеряют приборами электромагнитной, электродинамической и тепловой систем. 1.3. Символический метод расчета цепей переменного На рис 1.2 показано, что синусоидальная функция
Для любого момента времени
вектора;
Можно вести расчет не только с использованием комплексной амплитуды
тока. Метод расчета с использованием изображающих векторов или соответствующих им комплексных чисел называется символическим методом, т.к. действительные синусоидальные функции заменяют символами. Напряжение и ЭДС можно представить аналогичными изображающими комплексами
Совокупность векторов, построенная с соблюдением их взаимной ориентации по фазе, называется векторной диаграммой. Векторную диаграмму всегда изображают для момента
1.4. Основные законы электротехники в
|


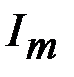









 . Направление тока, для которого его мгновенные значения положительны, называется положительным направлением тока. Ток определен, если известна зависимость его мгновенного значения от времени
. Направление тока, для которого его мгновенные значения положительны, называется положительным направлением тока. Ток определен, если известна зависимость его мгновенного значения от времени  и указано его положительное направление.
и указано его положительное направление.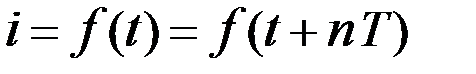 , где
, где  - целое число. В системе СИ единицы измерения [
- целое число. В системе СИ единицы измерения [  (рис.1.1а).
(рис.1.1а).







 ;
;  Гц (Герц)
Гц (Герц) называется амплитудой
называется амплитудой 
 к меньшему потенциалу
к меньшему потенциалу  .
.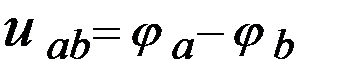 - положительное (по току);
- положительное (по току);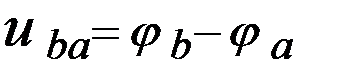 - отрицательное (навстречу току).
- отрицательное (навстречу току).
 .
. вектора
вектора 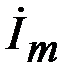 , развернутую во времени (рис.1.2). Аргумент синуса
, развернутую во времени (рис.1.2). Аргумент синуса  называется фазой колебания. Фаза характеризует состояние колебания, т.е. значение функции в данный момент времени
называется фазой колебания. Фаза характеризует состояние колебания, т.е. значение функции в данный момент времени  . Значение фазы при
. Значение фазы при  , т.е.
, т.е.  , есть начальная фаза синусоидального тока. Любая синусоидально изменяющаяся функция вполне определяется тремя параметрами: амплитудой
, есть начальная фаза синусоидального тока. Любая синусоидально изменяющаяся функция вполне определяется тремя параметрами: амплитудой 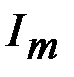 , угловой частотой
, угловой частотой  , начальной фазой
, начальной фазой  .
. - комплексная амплитуда синусоидального тока,
- комплексная амплитуда синусоидального тока, - амплитуда синусоидального тока,
- амплитуда синусоидального тока, - период синусоидальных колебаний,
- период синусоидальных колебаний,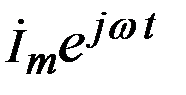
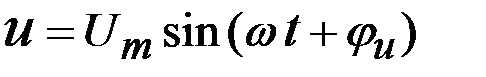 ;
;  .
. ;
; .
. ;
;  .
. ;
; .
. ;
;  .
. представляет собой проекцию на ось мнимых величин
представляет собой проекцию на ось мнимых величин  вектора длинною
вектора длинною  , т.е.
, т.е.  .
.  , называемым комплексной амплитудой.
, называемым комплексной амплитудой. - комплексная амплитуда, определяет величину и положение вектора при
- комплексная амплитуда, определяет величину и положение вектора при  .
. ;
; - действительная часть вращающегося
- действительная часть вращающегося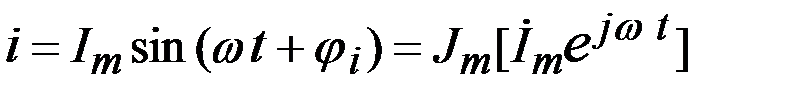 - мнимая часть вращающегося вектора, представляет собой мгновенное значение синусоидального тока.
- мнимая часть вращающегося вектора, представляет собой мгновенное значение синусоидального тока. , но и комплекса действующего значения тока
, но и комплекса действующего значения тока 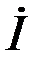 . Необходимо четко усвоить связь между следующими величинами:
. Необходимо четко усвоить связь между следующими величинами: - мгновенное значение синусоидального тока;
- мгновенное значение синусоидального тока; - действующее значение синусоидального тока;
- действующее значение синусоидального тока; - комплексная амплитуда синусоидального тока;
- комплексная амплитуда синусоидального тока; - комплекс действующего значения синусоидального
- комплекс действующего значения синусоидального ;
;  или векторами.
или векторами. , при этом начальную фазу соответствующего вектора откладывают от оси действительных чисел
, при этом начальную фазу соответствующего вектора откладывают от оси действительных чисел  (рис.1.3). Углы, отложенные против часовой стрелки - положительные, по часовой - отрицательные. На рис. 1.3
(рис.1.3). Углы, отложенные против часовой стрелки - положительные, по часовой - отрицательные. На рис. 1.3 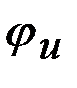 - положительный,
- положительный,  - отрицательный угол. Сдвиг по фазе тока относительно напряжения
- отрицательный угол. Сдвиг по фазе тока относительно напряжения  нужно показывать стрелкой от тока
нужно показывать стрелкой от тока  к напряжению
к напряжению 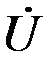 .
.  - положительный. Основные законы электротехники для цепей
- положительный. Основные законы электротехники для цепей