ЗАДАЧА 7
При анализе электромагнитных процессов в сердечниках трансформаторов и электромагнитах переменного тока, а также в участках магнитопроводов электрических машин, пронизываемых переменными магнитными потоками, необходимо учитывать, что перечисленные элементы конструкций собирают из листов электротехнической стали, разделенной изоляционными промежутками. Распределение переменного магнитного потока и потерь, обусловленных вихревыми токами, индуцированными потоками в заказанных элементах, в значительной степени определяют параметры устройства в целом. Анализ указанного распределения можно произвести на примере одного листа. Дан плоский лист из электротехнической стали толщиной 2 а и высотой h. Удельная электропроводность стали g = 107 См/м, а ее магнитная проницаемость равна m>>m0 = 4 p×10-7 Гн/м. Лист расположен вдоль линий векторов напряженности H и индукции B = m H магнитного поля (рис. 7.1), синусоидально изменяющегося во времени с частотой 1) получить (вывести, доказать) каждое из приведенных ниже соотношений (7.1)-(7.18); 2) рассчитать и показать на рис. 7.1 в масштабе толщины листа глубину проникновения s электромагнитного поля; 3) рассчитать потери Р на вихревые токи в листе длиной 1 м и модуль магнитного потока Ф, проходящего по листу; 4) рассчитать и построить график распределения модуля индукции В в сечении листа в зависимости от координаты z (расчеты выполнить для точек z = 0, ±а /2, ±а); 5) рассчитать аналогично п. 3 потери Р 0 и поток Ф0 в случае, когда магнитное поле является постоянным (f = 0), и сравнить их с величинами Р и Ф; 6) рассчитать и построить на графике п. 4 аналогичную зависимость от координаты z индукции B 0в случае, когда магнитное поле является постоянным (f = 0).
Таблица 7.1
Рис. 7.1
Указания
Для решения этой задачи сначала необходимо проработать материал, изложенный в [1], с. 147...155 или [2], с. 382…385. Векторы H и B имеют лишь по одной составляющей Нх и Вх по оси х, т. е.
Обычно высота листа h >> 2 а (рис. 7.1). В этом случае линии вектора J плотности вихревого тока можно считать прямыми, параллельными оси у. Следовательно, и вектор E = J g напряженности электрического поля будет иметь лишь одну составляющую по оси у:
Электромагнитное поле в листе описывается уравнениями Максвелла в комплексной форме:
где C учетом (7.1) и (7.2) уравнения (7.3), записанные в прямоугольных координатах х, y, z, принимают вид
Отсюда следует уравнение
где Общее решение уравнения (7.5) имеет вид
где Согласно рис. 7.1 напряженность (7.7) должна удовлетворять граничным условиям
из которых могут быть найдены значения
Разрешив систему двух алгебраических уравнений (7.9) относительно
где C учетом (7.10) из первого уравнения (7.4) следует
где Выражение (7.10) позволяет определить комплекс магнитной индукции:
Следовательно, искомый модуль индукции
С учетом рис. 7.1 и формул (7.10), (7.12) для комплекса магнитного потока
где Следовательно, искомый модуль потока
Модули от гиперболических функций в (7.13) и (7.15) могут быть найдены с помощью известных формул:
Для искомых потерь Р можно записать выражение
Отсюда с учетом (7.11) и (7.16) следует
Требуемые выражения для В 0, Ф0 и Р 0определяются как пределы выражений (7.13), (7.15) и (7.18) при w ® 0, когда, согласно (7.6) к ® 0. Так как sh (0)= sin(0)= 0, то при этом в (7.15) следует
|

 При этом действующее значение Н на обеих поверхностях листа равно H 0 . Используя данные табл. 7.1, требуется:
При этом действующее значение Н на обеих поверхностях листа равно H 0 . Используя данные табл. 7.1, требуется:


 ,
,  ,
, 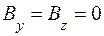 ,
,  . (7.1)
. (7.1) ,
,  ,
, 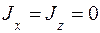 ,
,  . (7.2)
. (7.2) ,
,  ,
, 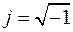 , (7.3)
, (7.3) и
и  - векторы напряженностей магнитного и электрического полей в комплексной форме.
- векторы напряженностей магнитного и электрического полей в комплексной форме. ,
,  . (7.4)
. (7.4) , (7.5)
, (7.5)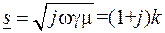 ,
,  . (7.6)
. (7.6)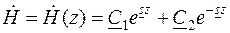 , (7.7)
, (7.7) и
и  - комплексные постоянные интегрирования.
- комплексные постоянные интегрирования. , (7.8)
, (7.8) . (7.9)
. (7.9) ,
,  , (7.10)
, (7.10) - гиперболический косинус.
- гиперболический косинус. ,
,  , (7.11)
, (7.11) - гиперболический синус.
- гиперболический синус. . (7.12)
. (7.12) . (7.13)
. (7.13) можно записать уравнения
можно записать уравнения ,
,  , (7.14)
, (7.14) - гиперболический тангенс.
- гиперболический тангенс. ,
,  . (7.15)
. (7.15) ,
,  (7.16)
(7.16) . (7.17)
. (7.17) . (7.18)
. (7.18) ®0 и
®0 и и затем найти предел выражения
и затем найти предел выражения  по правилу Лопиталя с учетом того, что sh ¢(
по правилу Лопиталя с учетом того, что sh ¢( a)= ch (
a)= ch (


