ЗАДАЧА 8
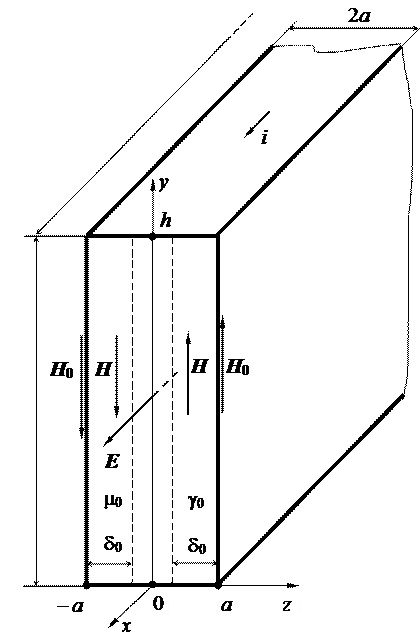
Многоамперные токоведущие системы и электрические аппараты, как правило, содержат медные и алюминиевые шины прямоугольного сечения. Переменный ток в поперечном сечении этих шин вследствие поверхностного эффекта распределяется неравномерно, что увеличивает их активное сопротивление R по сравнению с сопротивлением R 0 постоянному току (R > R 0). Пусть имеется, например, алюминиевая шина (рис. 8.1) толщиной 2 а и высотой h >> 2 а, имеющая удельную электропроводность g0 = 3,5 × 107 Cм/м и магнитную проницаемость m0=4p×107 Гн/м. По шине протекает синусоидальный ток i с частотой f = w/2p. Используя данные табл. 8.1, требуется: 1) получить (вывести, доказать, обосновать) каждое из приведенных ниже соотношений (8.1)-(8.16); 2) рассчитать и показать на рис. 8.1 двумя пунктирными линиями 3) рассчитать для шины длиной 1м активное сопротивление R, Таблица 8.1
Рис. 8.1
Указания Для решения этой задачи сначала необходимо проработать материал, изложенный в [1], с. 146…155 или [2], с. 361…366. Так как h >> 2 а, то вектор напряженности магнитного поля H в шине (рис. 8.1) практически будет иметь лишь одну составляющую Ну по оси у, т. е.
При этом вектор напряженности электрического поля E имеет только одну составляющую Ех по оси х, т. е.
Электромагнитное поле в шине описывается уравнением Максвелла в комплексной форме:
где С учетом (8.1) и (8.2) уравнения (8.3), записанные в прямоугольных координатах x, y, z, принимают вид
Отсюда следует уравнение
где
Общее решение уравнения (8.5) имеет вид
где Согласно рис. 8.1 и закону полного тока напряженность (8.7) должна удовлетворять граничным условиям
где I – действующее значение тока i, проходящего по шине. С учетом (8.7) уравнения (8.8) принимают вид
Разрешив систему двух алгебраических уравнений относительно
где С учетом (8.10) из первого уравнения (8.4) следует
где Искомое активное сопротивление
где Р – мощность тепловыделения в шине длиной 1м (рис. 8.1):
Согласно (8.11) подынтегральная функция в (8.13) преобразуется к виду (см. (7.16) в задаче 7):
С учетом (8.13), (8.14) и (8.8) из (8.12) находим
Сопротивление R 0 может быть получено как предел выражения (8.15) при w® 0 (см. пояснения к формуле (7.18) в задаче 7). Сопротивление R s фактически равно сопротивлению постоянному току 1 метра шины, когда она имеет ширину не 2а, а 2s0 (рис. 8.2), т. е.
Приближенные выражения R 0и R sимеют погрешности
|



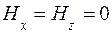 ,
, 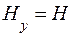 . (8.1)
. (8.1)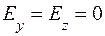 ,
, 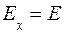 . (8.2)
. (8.2)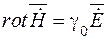 ,
,  ,
, 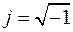 , (8.3)
, (8.3)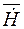 и
и  - векторы напряженностей магнитного и электрического полей в комплексной форме.
- векторы напряженностей магнитного и электрического полей в комплексной форме. ,
, 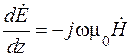 . (8.4)
. (8.4) , (8.5)
, (8.5)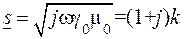 ,
, 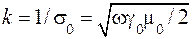 . (8.6)
. (8.6)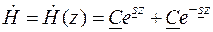 , (8.7)
, (8.7)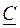 и
и 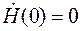 ,
, 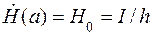 , (8.8)
, (8.8)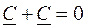 ,
, 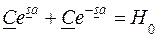 . (8.9)
. (8.9)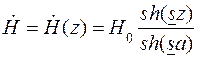 , (8.10)
, (8.10) - гиперболический синус (см. (7.11) в задаче 7).
- гиперболический синус (см. (7.11) в задаче 7).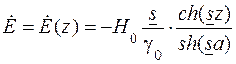 , (8.11)
, (8.11) - гиперболический косинус (см. (7.10) в задаче 7).
- гиперболический косинус (см. (7.10) в задаче 7). , (8.12)
, (8.12)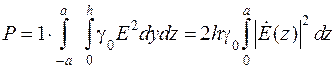 . (8.13)
. (8.13)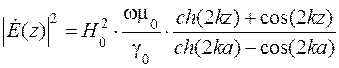 . (8.14)
. (8.14) ,
, 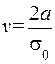 . (8.15)
. (8.15)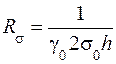 . (8.16)
. (8.16)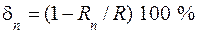 ,
, 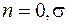 .
.


