ЗАДАЧА 6
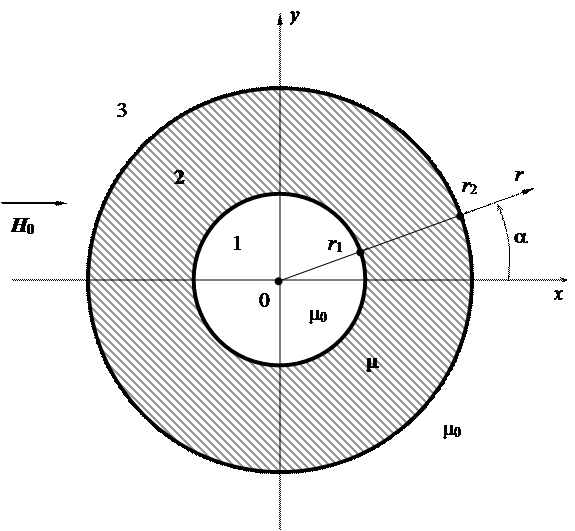
В современных приборах, машинах, аппаратах и автоматизированных комплексах наблюдается непрерывное повышение плотности заполнения объемов различными электромагнитными элементами, блоками и токове-дущими проводниками. В результате этого усиливается негативное электромагнитное влияние одних частей устройств на другие. Для ослабления такого влияния могут применяться различные электромагнитные экраны, например в виде труб, в полостях которых располагаются устройства, защищаемые от электрического, магнитного или электромагнитного полей. Пусть имеется магнитный экран, предназначенный для ослабления (экранирования) внешнего магнитного поля, причем экран представляет собой длинный полый ферромагнитный круговой цилиндр (трубу) с радиусами поверхностей r 1 и r 2 > r 1, характеризуемый усредненной постоянной магнитной проницаемостью m >> m0 = 4 p×10-7 Гн/м. Используя рис. 6.1 и данные табл. 6.1, требуется: 1) получить (вывести, доказать, обосновать) каждое из приведенных ниже соотношений (6.1)-(6.16); 2) рассчитать и показать на графике зависимость коэффициента экранирования К от толщины стенки цилиндра D = r 2 – r 1для значений D = 1,2,3,4 и 5 мм; 3) определить, во сколько раз уменьшится интенсивность магнитного поля внутри экрана при увеличении толщины его стенки в 5 раз? Во сколько раз при этом возрастет вес экрана?
Указания
Для решения этой задачи сначала необходимо проработать материал, изложенный в [1], с. 110…113 или [2], с. 293…302. Примем, что вектор напряженности Н 0 внешнего первичного однородного постоянного (т. е. неизменяющегося во времени) магнитного поля вне цилиндра (экрана) направлен вдоль оси х прямоугольных координат х, y, z (рис. 6.1). Это поле в цилиндрических координатах r, a, z может быть описано с помощью скалярного потенциала. Таблица 6.1
Рис. 6.1
где
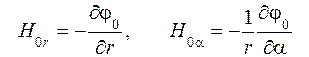 , ,
т. е. Н 0 есть величина напряженности внешнего магнитного поля. Результирующее магнитное поле, учитывающее влияние цилиндра, по аналогии с (6.1) можно также описать с помощью скалярного потенциала:
где r > r 2 (пространство вне цилиндра). Потенциал j n удовлетворяет уравнению Лапласа, которое в цилиндрических координатах с учетом независимости поля от переменной z имеет вид
Подставив (6.3) в (6.4), получим дифференциальное уравнение Эйлера:
общим решением которого является функция
где Сn и Dn - постоянные интегрирования. Примем, что на оси цилиндра (r = 0) потенциал равен нулю, т. е. согласно (6.3) и рис. 6.1
На большом же расстоянии от цилиндра (теоретически при r = µ) в соответствии с (6.1) и (6.3) должно выполняться условие
Кроме того, вследствие граничных условий в магнитном поле на обеих поверхностях цилиндра должны быть непрерывны касательные составляющие вектора напряженности Н, т. е. согласно рис. 6.1
На этих же поверхностях должны быть непрерывны и нормальные составляющие вектора магнитной индукции В, т. е.
С учетом (6.3) составляющие вектора Н будут равны
Подставив эти выражения в (6.9) и (6.10), получим
Отсюда с учетом (6.6) имеем
(6.13)
Кроме того, согласно (6.1), (6.2) и (6.3), (6.6) из (6.7) и (6.8) следует
С учетом (6.14) уравнения (6.13) фактически представляют собой разрешимую линейную алгебраическую систему 4-го порядка относительно постоянных интегрирования С 1 , С 2 , D 2 , D 3 . Однако согласно (6.16) для определения коэффициента экранирования К из системы (6.13) достаточно найти выражение для С 1 . Действительно, по определению
С учетом (6.6), (6.11) и (6.14) выражение (6.15) принимает вид
Подставив сюда выражение для С 1 и сократив Н 0 , можно получить формулу для расчета коэффициента экранирования как функции от радиусов цилиндра r 1, r 2 и относительной магнитной проницаемости
|

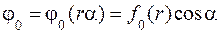 , (6.1)
, (6.1)
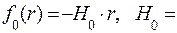 Н 0
Н 0 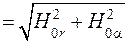 ,
,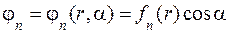 , n = 1, 2, 3, (6.3)
, n = 1, 2, 3, (6.3)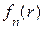 - искомые функции, причем согласно рис. 6.1 значение n = 1 соответствует области 1, где r < r 1 (полость цилиндра), значение n = 2 - области 2, где r 1 £ r £ r 2 (стенка цилиндра), а значение n = 3 – области 3, где
- искомые функции, причем согласно рис. 6.1 значение n = 1 соответствует области 1, где r < r 1 (полость цилиндра), значение n = 2 - области 2, где r 1 £ r £ r 2 (стенка цилиндра), а значение n = 3 – области 3, где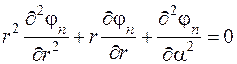 . (6.4)
. (6.4)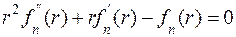 , (6.5)
, (6.5)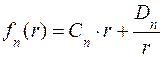 , (6.6)
, (6.6)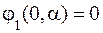 . (6.7)
. (6.7)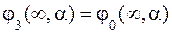 . (6.8)
. (6.8) (6.9)
(6.9)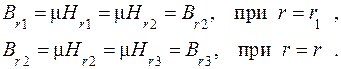 (6.10)
(6.10)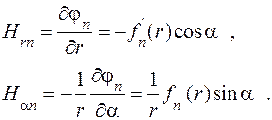 (6.11)
(6.11)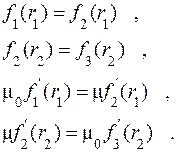 (6.12)
(6.12)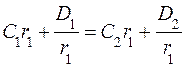 ,
, 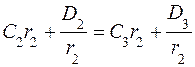 ;
;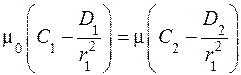 ,
, 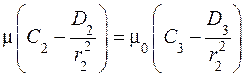 .
.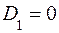 ,
, 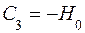 . (6.14)
. (6.14)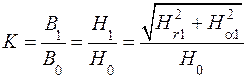 . (6.15)
. (6.15)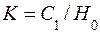 . (6.16)
. (6.16) m* = m / m0.
m* = m / m0.


