ЗАДАЧА 4. При изучении процессов в электрических цепях с распределенными параметрами рассматривался важный для практики случай двухпроводной линии электропередач
При изучении процессов в электрических цепях с распределенными параметрами рассматривался важный для практики случай двухпроводной линии электропередач. Электромагнитные процессы в такой линии определяются ее длиной и следующими параметрами, рассчитываемыми на единицу длины линии: электрической емкостью С между проводами и активной проводимостью утечки G между ними, обусловленной несовершенством воздуха как изолятора (удельная электропроводность воздуха g0 ¹ 0), индуктивностью L и активным сопротивлением R двух проводов. Через параметры C, G, L, R и угловую частоту wпитающего линию напряжения выражаются волновое сопротивление Z и коэффициент распространения d:
где величина aопределяет затухание тока и напряжения по длине линии и характеризует потери в ней (для линии без потерь a = 0); величина же b характеризует фазовые соотношения между напряжением и током в линии и определяет их фазовую скорость v = w / b. Формула (4.1) получена с помощью методов теории электрических цепей. Входящие же в них параметры С, G, R, L определяются как интегральные характеристики электромагнитного поля и поэтому могут быть рассчитаны только на основе теории поля. В настоящей задаче определению подлежат лишь два параметра: С и G. Пусть имеется двухпроводная линия (рис. 4.1), расположенная в воздухе с удельной электропроводностью g0 = 10-6 См/м и диэлектрической прони-цаемостью e0= 8,86×10-12 Ф/м. Ее провода 1 и 2 имеют одинаковые радиусы r 0 = 4 мм. Линия проходит параллельно плоской поверхности земли, имеющей удельную проводимость g >> g0 и диэлектрическую проницаемостью e >> e0 . Используя рис. 4.1 и данные табл. 4.1, требуется: 1) получить (вывести, доказать, обосновать) каждое из приведенных ниже соотношений (4.2)-(4.7); 2) рассчитать приближенные значения емкости С» С 0 и проводимости G» G 0 (без учета влияния земли); 3) рассчитать точные значения емкости С и проводимости G (с учетом влияния земли); 4) рассчитать относительные погрешности значений емкости С 0 и прово-димости G 0. Таблица 4.1
Рис. 4.1 Указания
Для решения этой задачи сначала необходимо проработать материал, изложенный в [1], с. 58, 59 или [2], с. 247…250. Согласно методу электростатической аналогии, справедливо соотно-шение
позволяющее по найденным значениям С рассчитать значения G. Вышеуказанная величина С 0 фактически соответствует емкости между двумя одинаковыми параллельными круговыми цилиндрами (рис. 4.1) радиусом r 0, оси которых отстоят друг от друга на расстоянии D 12. Следовательно,
Для нахождения значения С используем уравнения так называемых потенциальных коэффициентов. В рассматриваемом случае двухпроводной линии эти уравнения имеют вид
где j1 и j2 - потенциалы 1-го и 2-го проводов, t1 и t2 - их заряды на единицу длины, a11 и a22 – собственные коэффициенты, а a12 = a21 - взаимный потенциальный коэффициент. Так как e >> e0 и g >> g0 , то поверхность земли можно считать эквипотенциальной и имеющей, например, потенциал j = 0. Это позволяет для описания электрического поля над землей использовать метод зеркальных изображений (рис. 4.2), в соответствии с которым
 , ,  , ,
В двухпроводной линии
так что для искомой емкости С можно записать соотношение
Если теперь (4.4) подставить в (4.7), то с учетом (4.6) величина Искомые погрешности определяются выражением
Рис. 4.2
|

 ,
,  , (4.1)
, (4.1)


 , (4.2)
, (4.2) . (4.3)
. (4.3)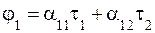 ,
, 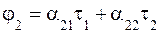 , (4.4)
, (4.4)
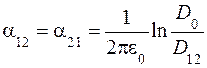 ,
, 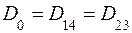 .
. , (4.6)
, (4.6) . (4.7)
. (4.7) сокращается и емкость С выражается только через коэффициенты (4.5), которые зависят от показанных на рис. 4.2 геометрических размеров.
сокращается и емкость С выражается только через коэффициенты (4.5), которые зависят от показанных на рис. 4.2 геометрических размеров. .
.







