ЗАДАЧА 9
Важнейшим параметром обмотки электрической машины является ее активное сопротивление. Последнее зависит от токораспределения в проводни-ках, расположенных в пазах машины. В случае крупной машины проводник может занимать целый паз, имея форму шины.
Пусть в открытом прямоугольном пазу машины расположена медная шина толщиной h и высотой а, имеющая удельную электропроводность g0 = 5,7×107 См/м и магнитную проницаемость m0= 4p×10-7 Гн/м. По шине протекает синусоидальный ток i с частотой f = w/2p. Толщина изоляции между шиной и пазом мала. Так как изоляция имеет ту же магнитную проницаемость m0, то можно считать, что ширина паза практически равна толщине h шины (рис. 9.1). Глубина же паза несколько больше высоты шины а. Используя данные табл. 9.1, требуется: 1) получить (вывести, доказать, обосновать) каждое из приведенных ниже соотношений (9.1)-(9.16); 2) рассчитать и показать на рис. 9.1 пунктирной линией в масштабе 3) рассчитать для шины длиной 1м активное сопротивление R,
Таблица 9.1
Указания Для решения этой задачи сначала необходимо изучить материал, изложенный в [1], с. 156 или [2], с. 361…366.
Так как материал паза (электротехническая сталь) характеризуется магнитной проницаемостью m >> m0,товектор напряженности магнитного поля в шине (рис. 9.1) практически будет иметь лишь одну составляющую Ну по оси у, т. е.
Рис. 9.1
При этом вектор напряженности электрического поля имеет только одну составляющую Ех по оси х, т. е.
Электромагнитное поле в шине описывается уравнениями Максвелла в комплексной форме:
где С учетом (9.1) и (9.2) уравнения (9.3), записанные в прямоугольных координатах х, у, z,принимают вид
где
Общее решение уравнения (9.5) имеет вид
где Так как m >> m0, то согласно рис. 9.1 и закону полного тока напряженность (9.7) должна удовлетворять граничным условиям
где I – действующее значение тока i, проходящего по шине. С учетом (9.7) уравнения (9.8) принимают вид
Разрешив систему двух алгебраических уравнений относительно и
где С учетом (9.10) и первого уравнения (9.4) следует
где Искомое активное сопротивление
где Р – мощность тепловыделения в шине длиной 1 м (рис. 9.1).
Согласно (9.11) подынтегральная функция в (9.13) преобразуется к виду (см. (7.16) в задаче 7):
С учетом (9.13), (9.14) и (9.8) из (9.12) находим
Сопротивление R 0 может быть получено как предел выражения (9.15) при w ® 0 (см. пояснения к формуле (7.18) в задаче 7). Сопротивление R s фактически равно сопротивлению постоянному току 1 метра шины, когда она имеет высоту не а,а s0 (рис. 9.1), т. е.
Приближенные выражения R 0 и R s имеют погрешности
|

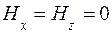 ,
, 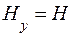 . (9.1)
. (9.1)




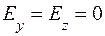 ,
, 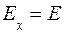 . (9.2)
. (9.2)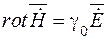 ,
,  ,
, 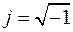 , (9.3)
, (9.3)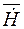 и
и  - векторы напряженностей магнитного и электрического полей в комплексной форме.
- векторы напряженностей магнитного и электрического полей в комплексной форме. ,
, 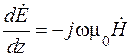 . (9.4)
. (9.4) Отсюда следует уравнение
Отсюда следует уравнение , (9.5)
, (9.5)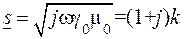 ,
, 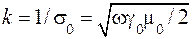 . (9.6)
. (9.6)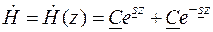 , (9.7)
, (9.7)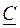 и
и 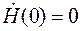 ,
,  , (9.8)
, (9.8)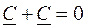 ,
, 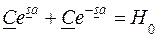 . (9.9)
. (9.9)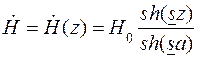 , (9.10)
, (9.10) - гиперболический синус (см. (7.10) в задаче 7).
- гиперболический синус (см. (7.10) в задаче 7).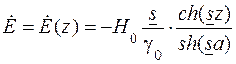 , (9.11)
, (9.11) - гиперболический косинус (см. (7.10) в задаче 7).
- гиперболический косинус (см. (7.10) в задаче 7). , (9.12)
, (9.12)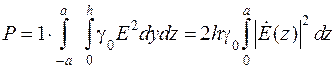 . (9.13)
. (9.13)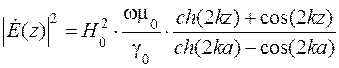 . (9.14)
. (9.14) ,
,  . (9.15)
. (9.15)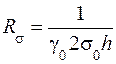 . (9.16)
. (9.16)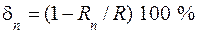 ,
, 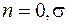 .
.


