ЗАДАЧА 2
Провод заземления подсоединен к металлической полусфере, погружен-ной в землю (рис. 2.1). Заданы: удельная электропроводность земли g, радиус полусферы r 0 и значение тока I короткого замыкания в проводе заземления (табл. 2.1). Требуется: 1) получить (вывести, доказать, обосновать) каждое из приведенных ниже соотношений (2.1)-(2.7);
2) рассчитать и построить графики изменения от координаты r напряжения Таблица 2.1

Рис. 2.1
Указания Для решения этой задачи сначала необходимо проработать материал, изложенный в [1], с. 75...78, 85, 86, пример 200, или [2], с. 276…279. Если второй электрод, к которому течет ток I от полусферы, находится достаточно далеко от нее, то вектор плотности тока J в земле будет иметь лишь одну радиальную составляющую (рис. 2.1):
где Соответственно этому вектор напряженности электрического поля Е будет также иметь одну радиальную составляющую Еr,которую можно определить из закона Ома в дифференциальной форме:
Теперь путем интегрирования уравнения
например, при условии, что
можно определить скалярный потенциал j =
или, следовательно,
Согласно рис. 2.1 напряжение
где Следовательно, величина
|

 на поверхности земли и шагового напряжения
на поверхности земли и шагового напряжения 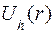 ; на осях указать размерности соответствующих величин; расчеты выполнить для точек r = r 0, r 0 + h/ 2, r 0+ h, r 0 + h, r 0 + 2 h, r 0 + 3 h, r 0 + 5 h, r 0 + 7 h, r 0 +10 h, считая, что расстояние шага равно h = 80 см.
; на осях указать размерности соответствующих величин; расчеты выполнить для точек r = r 0, r 0 + h/ 2, r 0+ h, r 0 + h, r 0 + 2 h, r 0 + 3 h, r 0 + 5 h, r 0 + 7 h, r 0 +10 h, считая, что расстояние шага равно h = 80 см.

 ,
, 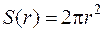 , (2.1)
, (2.1) - площадь поверхности полусферы радиусом r ³ r 0.
- площадь поверхности полусферы радиусом r ³ r 0. . (2.2)
. (2.2) , (2.3)
, (2.3) , (2.4)
, (2.4) :
: (2.5)
(2.5)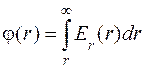 . (2.6)
. (2.6) ,
,  , (2.7)
, (2.7) есть напряжение на заземлителе.
есть напряжение на заземлителе.


