Решение. 1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств по формуле (12):

1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств по формуле (12):

П(1+i_k) ^{n k} = (1+0,3)² *(1+0,28) * (1+0,25)=2,704.

2-й вариант. Для выполнения расчетов по формулам воспользуемся функцией ПРОИЗВЕД (находится в категории Математические). Данная функция возвращает результат возведения в степень, рис.5.

а)

б)

Рис. 5. Результаты расчета множителя наращения (рис. а) и вид диалогового окна ПРОИЗВЕД с введенными данными (рис. б). В ячейку J4 введена формула =ПРОИЗВЕД((1+B3+D3)^F3;(1+B4+D4)^F4;(1+B5+D5)^F5)

 

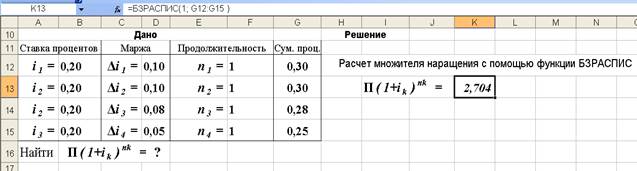
3-й вариант. Предварительно следует подготовить исходные данные по форме представленной на рис. 6а.Для выполнения расчетов следует воспользоваться функцией БЗРАСПИС (находится в категории Финансовые). Данная функция возвращает будущее значение основного капитала после начисления сложных процентов с переменной ставкой, рис.6. Поскольку здесь рассчитывается множитель наращения, то в качестве первоначальной суммы вводится 1 (см. рис 6).

а)

б)

Рис. 6. Результаты расчета множителя наращения (рис. а) и вид диалогового окна БЗРАСПИС с введенными данными (рис. б). В ячейку J13 введена формула =БЗРАСПИС(1; G12:G15)

 

Синтаксис функции БЗРАСПИС (первичное; план). Аргументы функции:

первичное – действительное число, задающее первоначальную стоимость инвестиции;

план – массив значений, содержащих процентные ставки.

Напомним, что для вычисления будущей стоимости с постоянной ставкой используется функция БС.

 

Пример 4. Ссуда 20 000 000 руб. предоставлена на 28 месяцев. Проценты сложные, ставка 18% годовых. Проценты начисляются ежеквартально. Вычислить наращенную сумму по истечении срока.

Известно:

P = 20 000 000 руб.,

j = 0,18 или 18%,

n = 28 месяцев = 28/12 лет,

m = 4.

Найти S =?

Решение.

1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств по формуле (13).

Всего за n лет имеем N = mn = 4*(28/12) = 28/3 периодов начислений при ежеквартальном (m = 4) начислении процентов в году. По формуле (13) находим: S = 20 000 000 * (1+ 0,18 / 4) ^(28/3) = 30 161 206,25 руб.

2-й вариант. Для выполнения расчетов воспользуемся функцией СТЕПЕНЬ (из категории Математические). Данная функция возвращает результат возведения в степень, рис.7.

 

Рис. 7. Результаты расчета наращенной суммы по номинальной ставке. В ячейку H3 введена формула =B2*СТЕПЕНЬ(1+B4/4;C3)

 

3-й вариант. Вычисления с помощью встроенных функций Excel. Для выполнения расчетов воспользуемся функцией БС (см. категорию Финансовые). Результаты расчета приведены на рис. 8.

 

Рис. 8. Результаты расчета наращенной суммы S по номинальной ставке с использованием финансовой функции БС. В ячейку H4 введена формула =БС(B4/4;C3;;-B2).

 

При финансовом анализе широко используется понятие эффективной ставки. Чем выше эффективная ставка финансовой операции, тем при прочих равных условиях она выгоднее кредитору.

 

Пример 5. Вычислить эффективную ставку процента, если банк начисляет проценты ежеквартально, исходя из номинальной ставки в 16% годовых.

Известно:

j = 0,16 или 16%.

Найти i _э =?