Формула Гаусса. (Лабораторная работа №7)
В квадратурной формуле Гаусса
узлы
где Если подынтегральная функция достаточно гладкая, то формула Гаусса обеспечивает очень высокую точность при небольшом числе узлов. В лабораторной работе №7 требуется, используя квадратурную формулу Гаусса наивысшего порядка точности, вычислить приближенное значение заданного интеграла. Интеграл предлагается вычислить по квадратурной формуле Гаусса с восемью узлами:
Порядок выполнения лабораторной работы №7. 1) Составить программу-функцию для вычисления интеграла по формуле Гаусса. 2) Составить программу-функцию для вычисления значений подынтегральной функции. 3) Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. 4) Результаты работы оформить в виде краткого отчета, содержащего характеристику используемого метода вычислений, его точности и полученное значение интеграла. Варианты заданий к лабораторной работе приведены в таблице 4.2.
|

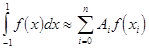
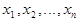 и коэффициенты
и коэффициенты 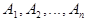 подобраны так, чтобы формула была точна для всех многочленов степени
подобраны так, чтобы формула была точна для всех многочленов степени 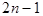 . Для приближенного вычисления интеграла по конечному отрезку
. Для приближенного вычисления интеграла по конечному отрезку 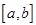 выполняется замена переменной
выполняется замена переменной 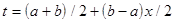 ; тогда квадратурная формула Гаусса принимает вид [2,8,12]
; тогда квадратурная формула Гаусса принимает вид [2,8,12]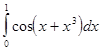

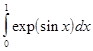
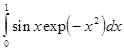
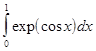
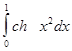
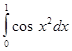
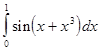
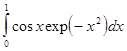
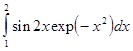
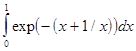
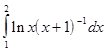
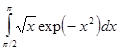
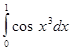

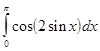
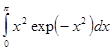

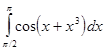
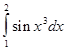

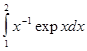
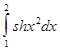

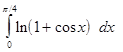
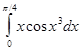
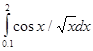
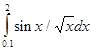
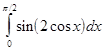
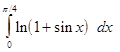
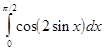
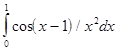
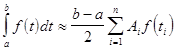 ,
,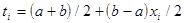 ;
; 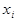 - узлы квадратурной формулы Гаусса;
- узлы квадратурной формулы Гаусса; 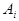 - гауссовы коэффициенты
- гауссовы коэффициенты 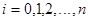 .
.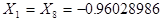 ,
, 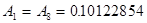 ;
; ,
, 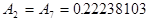 ;
;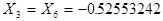 ,
, 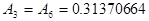 ;
;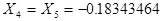 ,
, 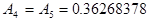 .
.


