Метод простых итераций
(Лабораторная работа №6)
Метод простых итераций решения уравнения Рассмотрим один шаг итерационного процесса. Исходя из найденного на предыдущем шаге значения xn-1, вычисляется y= j(xn-1). Если Для применения метода простых итераций определяющее значение имеет выбор функции В лабораторной работе № 6 предлагается, используя программы-функции ITER и Round из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения Для данной работы вид функции Порядок выполнения лабораторной работы №6 должен быть следующим. 1) Графически или аналитически отделить корень уравнения 2) Преобразовать уравнение 3) Выбрать начальное приближение, лежащее на [Left, Right]. 4) Составить подпрограмму для вычисления значений 5) Составить головную программу, вычисляющую корень уравнения и содержащую обращение к программам 6) Провести вычисления по программе. Исследовать скорость сходимости и обусловленность метода. Текст программы - функции ITER, позволяющей вычислять корни уравнения x=
Курсовая работа по дисциплине и варианты заданий
Лабораторные работы, описанные в настоящем разделе, целесообразно объединять для выполнения курсовой работы, нацеленной на сравнительную оценку различных методов приближенного решения нелинейных уравнений. Типовое задание на курсовую работу формулируется следующим образом. Задание на курсовую работу по дисциплине "Вычислительная математика". Используя программы - функции BISECT, NEWTON, HORDA, ITER, Round из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения Исследуйте обусловленность методов и зависимость числа итераций от точности результата Eps при изменении Eps от 0.0 до 0.000001. Порядок выполнения курсовой работы Графически или аналитически отделить корень уравнения Составить подпрограмму- функцию вычисления функции Составить головную программу, содержащую ввод исходных данных, обращение к подпрограммам BISECT, NEWTON, HORDA, ITER вывод результатов. Выполнить вычисления по программе. Построить графики зависимости числа итераций, необходимых для достижения заданной точности Eps, от величины Eps, а также достижимой точности результатов от точности Delta задания функции Теоретически и экспериментально сравнить методы бисекции, Ньютона, хорд и итераций по скорости сходимости и степени обусловленности. Результаты оформить в виде отчета, содержащего постановку задачи, тексты разработанных программ, результаты теоретического и экспериментального анализа в виде таблиц и графиков, выводы. Вид функции
|

 состоит в замене исходного уравнения эквивалентным ему уравнением x=j(x) и построении последовательности xn+1=j(xn), сходящейся при n®¥ к точному решению. Достаточные условия сходимости метода простых итераций формулируются теоремой, приведенной [1,2,7].
состоит в замене исходного уравнения эквивалентным ему уравнением x=j(x) и построении последовательности xn+1=j(xn), сходящейся при n®¥ к точному решению. Достаточные условия сходимости метода простых итераций формулируются теоремой, приведенной [1,2,7]. , то полагается xn=y и выполняется очередная итерация. Если же
, то полагается xn=y и выполняется очередная итерация. Если же  , то вычисления заканчиваются и за приближенное значение корня принимается величина xn=y. Погрешность результата вычислений зависит от знака производной
, то вычисления заканчиваются и за приближенное значение корня принимается величина xn=y. Погрешность результата вычислений зависит от знака производной  : при
: при  в уравнении
в уравнении 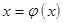 , эквивалентном исходному. Функцию
, эквивалентном исходному. Функцию 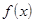 тем выше, чем выше число q.
тем выше, чем выше число q. ,
,  для любой функции, которая удовлетворяет достаточным условиям сходимости метода, приводится ниже.
для любой функции, которая удовлетворяет достаточным условиям сходимости метода, приводится ниже. с заданной точностью методом бисекции, Ньютона, хорд и итераций соответственно.
с заданной точностью методом бисекции, Ньютона, хорд и итераций соответственно. удовлетворяет условиям применимости методов).
удовлетворяет условиям применимости методов). (при необходимости), предусмотрев округление их значений с заданной точностью Delta с использованием библиотечной функции Round.
(при необходимости), предусмотрев округление их значений с заданной точностью Delta с использованием библиотечной функции Round. ;
;
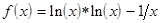
 ;
;
 ;
;
 ;
;
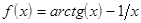 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
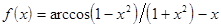 ;
;
 ;
;
 ;
;
 ;
;
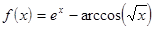 ;
;
 ;
;
 ;
;
 ;
;



