(Лабораторная работа № 5)
В случае, когда известно хорошее начальное приближение решения уравнения  , эффективным методом повышения точности является метод Ньютона. Он состоит в построении итерационной последовательности
, эффективным методом повышения точности является метод Ньютона. Он состоит в построении итерационной последовательности  сходящейся к корню уравнения
сходящейся к корню уравнения  . Достаточные условия сходимости метода формулируются теоремой, приведенной в [1,7].
. Достаточные условия сходимости метода формулируются теоремой, приведенной в [1,7].
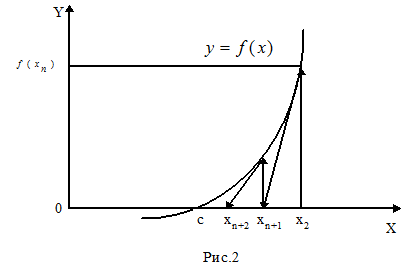
Метод Ньютона допускает простую геометрическую интерпретацию (рис. 2). Если через точку с координатами  провести касательную, то абсцисса точки пересечения этой касательной с осью Ох будет очередным приближением xn+1 корня уравнения
провести касательную, то абсцисса точки пересечения этой касательной с осью Ох будет очередным приближением xn+1 корня уравнения  .
.
Для оценки погрешности n-го приближения корня предлагается пользоваться неравенством
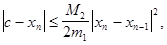
где М2-наибольшее значение модуля второй производной  на отрезке [a,b]; m1-наименьшее значение модуля первой производной
на отрезке [a,b]; m1-наименьшее значение модуля первой производной  на отрезке [a,b]. Таким образом, если
на отрезке [a,b]. Таким образом, если  то
то  Это означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро (имеет место квадратическая сходимость). Из указанного следует, что при необходимости нахождения корня с точностью e итерационный процесс можно прекращать, когда
Это означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро (имеет место квадратическая сходимость). Из указанного следует, что при необходимости нахождения корня с точностью e итерационный процесс можно прекращать, когда
 (3.1)
(3.1)
Рассмотрим один шаг итераций. Если на (n-1)-м шаге очередное приближение xn-1 не удовлетворяет условию окончания процесса, то вычисляются величины  и следующие приближение корня
и следующие приближение корня  При выполнении условия (3.1) величина xn принимается за приближенное значение корня с, вычисленное с точностью e.
При выполнении условия (3.1) величина xn принимается за приближенное значение корня с, вычисленное с точностью e.
В лабораторной работе № 5 предлагается, используя программы-функции NEWTON и ROUND из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения  с заданной точностью Eps методом Ньютона, исследовать скорость сходимости и обусловленность метода.
с заданной точностью Eps методом Ньютона, исследовать скорость сходимости и обусловленность метода.
Для данной работы вид функции 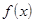 задается индивидуально каждому студенту преподавателем из числа вариантов, приведенных в подразделе 3.6.
задается индивидуально каждому студенту преподавателем из числа вариантов, приведенных в подразделе 3.6.
Порядок выполнения лабораторной работы №5.
1) Графически или аналитически отделить корень уравнения  (т.е. найти отрезки [Left, Right], на котором функция
(т.е. найти отрезки [Left, Right], на котором функция 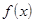 удовлетворяет условиям сходимости метода Ньютона).
удовлетворяет условиям сходимости метода Ньютона).
2) Составить подпрограммы - функции вычисления 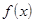 ,
,  , предусмотрев округление их значений с заданной точностью Delta.
, предусмотрев округление их значений с заданной точностью Delta.
3) Составить головную программу, вычисляющую корень уравнения  и содержащую обращение к подпрограммам,
и содержащую обращение к подпрограммам, 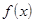 ,
,  (x), Round, NEWTON и индикацию результатов.
(x), Round, NEWTON и индикацию результатов.
4) Выбрать начальное приближение корня x0 из [Left, Right] так, чтобы 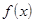
 >0.
>0.
5) Провести вычисления по программе. Исследовать скорость сходимости метода и чувствительность метода к ошибкам в исходных данных.
Для приближенного вычисления корней уравнения  методом Ньютона предназначена программа - функция NEWTON, текст которой представлен в подразделе 3.7.
методом Ньютона предназначена программа - функция NEWTON, текст которой представлен в подразделе 3.7.

 , эффективным методом повышения точности является метод Ньютона. Он состоит в построении итерационной последовательности
, эффективным методом повышения точности является метод Ньютона. Он состоит в построении итерационной последовательности  сходящейся к корню уравнения
сходящейся к корню уравнения 
 провести касательную, то абсцисса точки пересечения этой касательной с осью Ох будет очередным приближением xn+1 корня уравнения
провести касательную, то абсцисса точки пересечения этой касательной с осью Ох будет очередным приближением xn+1 корня уравнения 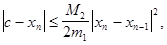
 на отрезке [a,b]; m1-наименьшее значение модуля первой производной
на отрезке [a,b]; m1-наименьшее значение модуля первой производной  на отрезке [a,b]. Таким образом, если
на отрезке [a,b]. Таким образом, если  то
то  Это означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро (имеет место квадратическая сходимость). Из указанного следует, что при необходимости нахождения корня с точностью e итерационный процесс можно прекращать, когда
Это означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро (имеет место квадратическая сходимость). Из указанного следует, что при необходимости нахождения корня с точностью e итерационный процесс можно прекращать, когда (3.1)
(3.1) и следующие приближение корня
и следующие приближение корня  При выполнении условия (3.1) величина xn принимается за приближенное значение корня с, вычисленное с точностью e.
При выполнении условия (3.1) величина xn принимается за приближенное значение корня с, вычисленное с точностью e.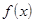 задается индивидуально каждому студенту преподавателем из числа вариантов, приведенных в подразделе 3.6.
задается индивидуально каждому студенту преподавателем из числа вариантов, приведенных в подразделе 3.6. , предусмотрев округление их значений с заданной точностью Delta.
, предусмотрев округление их значений с заданной точностью Delta. (x), Round, NEWTON и индикацию результатов.
(x), Round, NEWTON и индикацию результатов.


