Метод бисекции
(Лабораторная работа №3)
Если найден отрезок [a,b], такой, что Рассмотрим один шаг итерационного процесса. Пусть на (n-1)-м шаге найден отрезок [an-1, bn-1]Ì[a, b], такой, что an=an-1, bn=x, если an=x, bn= bn-1, если Если требуется найти корень с точностью e, то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше 2e. Тогда координата середины отрезка есть значение корня с требуемой точностью e. Метод бисекции является простым и надежным методом поиска простого корня уравнения В лабораторной работе №3 предлагается, используя программы - функции BISECT и Round из файла methods.cpp (файл заголовков metods.h, директория LIBR1), найти корень уравнения Выполнение работы осуществляется по индивидуальным вариантам заданий (нелинейных уравнений), приведенным в подразделе 3.6. Номер варианта для каждого студента определяется преподавателем. Порядок выполнения работы должен быть следующим: 1) Графически или аналитически отделить корень уравнения 2) Составить подпрограмму вычисления функции 3) Составить головную программу, содержащую обращение к подпрограмме f(x), BISECT, Round и индикацию результатов. 4) Провести вычисления по программе. Построить график зависимости числа итераций от Eps. 5) Исследовать чувствительность метода к ошибкам в исходных данных. Ошибки в исходных данных моделировать с использованием программы Round, округляющей значения функции с заданной точностью Delta. Текст программы-функции BISECT, предназначенной для решения уравнения
|

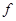 (a)
(a) 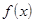 (корень уравнения
(корень уравнения  с любой заданной точностью.
с любой заданной точностью.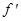 (с)¹0). Этот метод сходится для любых непрерывных функций
(с)¹0). Этот метод сходится для любых непрерывных функций 


