Метод хорд
(Лабораторная работа №4)
Пусть найден отрезок [a, b], на котором функция
Сначала находится уравнение хорды АВ:
Для точки пересечения ее с осью абсцисс (x=c0, y=0) получается уравнение
Далее сравниваются знаки величин Алгоритмы методов бисекции и хорд похожи, однако метод хорд в ряде случаев дает более быструю сходимость итерационного процесса, причем успех его применения, как и метода бисекции, гарантирован. В лабораторной работе №4 предлагается, используя программы - функции HORDA и Round из файла methods.cpp (файл заголовков metods.h, директория LIBR1), найти корень уравнения Для данной работы, как и для лабораторной работы №3 задаются индивидуальные варианты нелинейных уравнений (см. подраздел 3.6). Порядок выполнения лабораторной работы №4: 1) Графически или аналитически отделить корень уравнения 2) Составить подпрограмму - функцию вычисления функции 3) Составить головную программу, вычисляющую корень уравнения 4) Провести вычисления по программе. Теоретически и экспериментально исследовать скорость сходимости и обусловленность метода. В подразделе 3.7 приводится текст программы - функции HORDA, предназначенной для решения уравнения
|

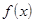 меняет знак. Для определенности положим
меняет знак. Для определенности положим 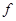 (a)>0,
(a)>0,  принимаются значения c0, c1,... точек пересечения хорды с осью абсцисс, как это показано на рис.1.
принимаются значения c0, c1,... точек пересечения хорды с осью абсцисс, как это показано на рис.1.





