ЧАСТНЫЕ ПРОИЗВОДНЫЕ.
1. Понятие производной, ее механический и геометрический смысл. а ) Приращение аргумента и функции. Пусть дана функция y=f(х), где х– значение аргумента из области определения функции. Если выбрать два значения аргумента хои х из определенного интервала области определения функции, то разность между двумя значениями аргумента называется приращением аргумента: х - хо=∆х. Значение аргумента x можно определить через x0и его приращение: х = хо+ ∆х. Разность между двумя значениями функции называется приращением функции: ∆y =∆f = f(хо+∆х) – f(хо).
1) даем аргументу приращение ∆х и получаем значение – x+Δx; 2) находим значение функции для значения аргумента (х+∆х) – f(х+∆х); 3) находим приращение функции ∆f=f(х + ∆х) - f(х). Пример:Определить приращение функции y=х2, если аргумент изменился от хо=1 до х=3. Для точки хо значение функции f(хо)=х²о; для точки (хо+∆х) значение функции f(хо+∆х) = (хо+∆х)2 = х²о+2хо∆х+∆х2, откуда ∆f = f(хо+∆х)–f(хо) = (хо+∆х)2–х²о = х²о+2хо∆х+∆х2–х²о = 2хо∆х+∆х2; ∆f = 2хо∆х+∆х2; ∆х = 3–1 = 2; ∆f =2·1·2+4 = 8. б) Задачи, приводящие к понятию производной. Определение производной, ее физический смысл. Понятие приращения аргумента и функции необходимы для введения понятия производной, которое исторически возникло исходя из необходимости определения скорости тех или иных процессов. Рассмотрим, каким образом можно определить скорость прямолинейного движения. Пусть тело движется прямолинейно по закону: ∆Ѕ= J·∆t. Дляравномерного движения: J = ∆Ѕ/∆t. Для переменного движения значение ∆Ѕ/∆tопределяет значение Jср., т.е. Jср. =∆Ѕ/∆t.Но средняя скорость не дает возможности отразить особенности движения тела и дать представление об истинной скорости в момент времени t. При уменьшении промежутка времени, т.е. при ∆t→0 средняя скоростьстремится к своему пределу – мгновенной скорости: Jмгн.= Таким же образом определяется и мгновенная скорость химической реакции: Jмгн.= где х – количество вещества, образовавшееся при химической реакции за время t. Подобные задачи по определению скорости различных процессов привели к введению в математике понятия производной функции. Пусть дана непрерывная функция f(х),определенная на интервале ]а,в[иее приращение ∆f=f(х+∆х)–f(х).Отношение Предел отношения y'x= Производная обозначается: Исходя из определения производной, можно сказать, что мгновенная скорость прямолинейного движения есть производная от пути по времени: Jмгн.= S't = f ' (t). Таким образом, можно сделать вывод, что производная функции по аргументу х есть мгновенная скорость изменения функции f(х): у'x = f ' (х)= Jмгн. В этом и заключается физический смысл производной. Процесс нахождения производной называется дифференцированием, поэтому выражение «продифференцировать функцию» равносильно выражению «найти производную функции». в) Геометрический смысл производной.
к = tgα = г) Общее правило нахождения производной. Исходя из определения производной, процесс дифференцирования функции можно представить следующим образом: 1) выбрав некоторое значение аргумента х, дают ему приращение f(х+∆х) = f(х)+∆f; 2) находят приращение функции: ∆f = f(х + ∆х) - f(х); 3) составляют отношение приращения функции к приращению аргумента:
4) находят предел отношения Пример:f(х)=х2; f ' (х)=?. 1) f(х +∆х) = (х+∆х)2; 2) ∆f = f(х+∆х)-f(х) = (х+∆х)2-х2 = х2+2х∆х+∆х2-х2 = 2х ∆х+∆х2; 3) 4) f ' (х) = 5) f ' (х) = 2х. Однако, как видно даже из этого простого примера, применение указанной последовательности при взятии производных – процесс трудоемкий и сложный. Поэтому для различных функций вводятся общие формулы дифференцирования, которые представлены в виде таблицы «Основных формул дифференцирования функций». 2. Производная сложной функции.
Функция является сложной, если она может быть представлена в виде функции от функции у = f[φ(х)], где у = f(u), а u = φ(х), где u - промежуточный аргумент. Любую сложную функцию можно представить в виде элементарных функций (простых), которые являются ее промежуточными аргументами. Примеры: Простые функции: Сложные функции: у= х2 у = (х+1)2; u = (х+1); у= u2; у = sin x; у = sin 2x; u = 2х; у = sin u; у = ех у = е2х; u = 2х; у = еu; у = ln х у = ln (х+2); u = х+2; у = ln u. Общее правило дифференцирования сложной функции дается приведённой теоремой без доказательства. Если функция u = φ(х) имеет производную u'x = φ'(х) в точке х, а функция у = f(u) производную у'u = f ' (u) в соответствующей точке u, то производная сложной функции у = f[φ(х)] в точке х находится по формуле: у'х = f ' (u) · u'(х). Часто используется менее точная, но более короткая формулировка данной теоремы: производная сложной функции равна произведению производной по промежуточной переменной на производную промежуточной переменной по независимой переменной. Пример: у = sin 2x2; u = 2х2; у = sin u; у'х = (sin u)'u · (2x2)'х = cos u · 4х = 4х · cos 2х2.
3. Производная второго порядка. Механический смысл второй производной.
Производную функции у =f(х) называют производной первого порядка или просто первой производной функции. Эта производная является функцией от х и её можно дифференцировать вторично. Производная от производной называется производной второго порядка или второй производной. Она обозначается: у"хх– (игрек два штриха поикс);f"(х) – ( эф два штрих по икс); d2у/dх2 – (дэ два игрек по дэ икс дважды); d2f/dх2 – (дэ два эф по дэ икс дважды). Исходя из определения второй производной, можно записать: у"хх = (у'х)'х; f"(х) = [f'(х)]'x d2у/dх2 = d/dх (dу/dх). Вторая производная в свою очередь есть функция от х и ее можно дифференцировать и получить производную третьего порядка и т.д. Пример: у = 2х3+х2; у"хх = [(2х3+х2)'x]'x = (6х2+2х)'x = 12х+2; Механический смысл второй производной объясняется на основе мгновенного ускорения, которым характеризуют переменное движение. Если S = f(t) – уравнение движения, то J = S't; а ср. = а мгн.= Таким образом, вторая производная от пути по времени равна мгновенному ускорению переменного движения. В этом и заключается физический (механический) смысл 2-ой производной. Пример:Пусть прямолинейное движение материальной точки происходит по закону S =t3/3. Ускорение материальной точки будет определяться как вторая производная S"tt: а = S"tt = (t3/3)" = 2t.
4. Дифференциал функции.
С понятием производной тесно связано понятие дифференциала функции, которое имеет важное практическое применение. Функция f(х) имеет производную Согласно теореме (теорему не рассматриваем) о связи бесконечно малой величины α(∆х)( Из последнего равенства следует, что приращение функции состоит из суммы, каждое слагаемое которой есть бесконечно малая величина при ∆х→ 0. Определим порядок малости каждой бесконечно малой величины этой суммы по отношению к бесконечно малой ∆х: 1) Следовательно, бесконечно малые f (х) ∆хи ∆химеют одинаковый порядок малости. 2) Следовательно, бесконечно малая величина α(∆х)∆х имеет более высокий порядок малости по отношению к бесконечно малой величине ∆х. Это означает, что в выражениях для ∆f второе слагаемое α(∆х)∆х быстрее стремится к 0 при ∆х→0, чем первое слагаемое f ' (х)∆х. Это первое слагаемое f ' (х)∆х называют дифференциалом функции в точке х. Он обозначаетсяdy (дэ игрек) или df (дэ эф). Итак,dy=df= f ' (х)∆х или dy = f ' (х) dх, т.к. дифференциал dх аргумента равен его приращению ∆х (если в формуле df = f ' (х)dх принять, что f(х)=х, то получим df = dx = x'х∆x, но x'х =1, т.е. dx =∆х). Итак, дифференциал функции равен произведению этой функции на дифференциал аргумента. Аналитический смысл дифференциала заключается в том, что дифференциал функции – есть главная часть приращения функции ∆f, линейная относительно аргумента ∆х.Дифференциал функции отличается от приращения функции на бесконечно малую величину α(∆х)∆х более высокого порядка малости, чем ∆х.Действительно ∆f=f ' (х)∆х+α(∆х)∆х или ∆f = df +α(∆х)∆х; откуда df = ∆f - α(∆х)∆х. Пример: у = 2х3 +х2; dу =? dу = у'dх = (2х3+х2)'xdx = (6х2 +2х)dx. Пренебрегая бесконечно малой величиной α(∆х)∆х более высокого порядкамалости, чем∆ х, получимdf ≈ ∆f ≈ f ' (х)dх т.е. дифференциал функции может быть использован для приближенного вычисления приращения функции, так как дифференциал обычно вычислять проще. Дифференциал может быть применен и к приближенному вычислению значения функции. Пусть нам известна функция y = f(х) и ее производная в точке х. Необходимо найти значение функции f(х+∆х) в некоторой близкой точке (х+∆х). Для этого воспользуемся приближенным равенством ∆у ≈ dy или ∆у ≈ f ' (х) · ∆х. Учитывая, что ∆у=f(х+∆х)-f(х), получим f(х+∆х)-f (х) ≈ f ' (х) · dх, откуда f(х+∆х) = f(х)+f ' (х) · dх. Полученная формула решает поставленную задачу. 5. Функции многих переменных. Частные производные и дифференциалы.
Большинство процессов, явлений в окружающем нас мире определяются не одной независимой переменной, а несколькими, функционально связанными между собой. Для изучения подобных зависимостей введено понятие функции нескольких аргументов. Например, S= ав (площадь); V= авс (объем), PV=RT; P=R В этих случаях часто возникает необходимость определить скорость указанных процессов и другие физические характеристики. Для функции двух или нескольких переменных рассматриваются вместо обычных производных – частные производные. Пусть дана некоторая функция двух аргументов z=f(х,у). Если мы дадим приращение только одному аргументу, например х, а второй аргумент yзафиксируем, то можно получить частное приращение функции по этому аргументу ∆ х f(х,у) = f(х+∆х,у)-f(х,у). Аналогично разность ∆уf(х,у)= f(х,у+∆у)-f(х,у) называется частным приращением функции z=f(х,у) по аргументу у. Частной производной функции двух независимых переменных z=f(х,у) называется производная, взятая по одному из аргументов, а второй аргумент при этом считается постоянным. Например, частная производная функции z=f(х,у) по аргументу х называется предел
По аналогии с дифференциалом функции одной независимой переменной частные дифференциалы функции по хи по у будут равны: dxz = Полный дифференциал функции двух независимых переменных будет равен сумме частных дифференциалов: dz = dxz + dyz = Полный дифференциал функции двух независимых переменных является главной частью полного приращения и может быть использован для приближенных расчетов полного приращения функции z=f(х,у), т.е. ∆f ≈ df; ∆z = ∆f ≈ Абсолютная величина полного приращения функции Объем цилиндра определяется по формуле V=πR2h, т.е. V=f(R,h). Необходимо определить приращение объема, если R и h получают приращения ∆h и ∆R. В этом случае: ∆V = dV = Пример: Найти частные производные и полный дифференциал функции: Z = 3х3у2 + х2у2 + у4
dz = dxz +dyz = ЛЕКЦИЯ №2
|

 Приращение аргумента и функции можно представить графически (рис.1). Приращение аргумента и приращение функции может быть как положительным, так и отрицательным. Как следует из рис.1 геометрически приращение аргумента ∆х изображается приращением абсциссы, а приращение функции ∆у – приращением ординаты. Вычисление приращения функции следует проводить в следующем порядке:
Приращение аргумента и функции можно представить графически (рис.1). Приращение аргумента и приращение функции может быть как положительным, так и отрицательным. Как следует из рис.1 геометрически приращение аргумента ∆х изображается приращением абсциссы, а приращение функции ∆у – приращением ординаты. Вычисление приращения функции следует проводить в следующем порядке: Jср.=
Jср.=  является функцией ∆х и выражает среднюю скорость изменения функции.
является функцией ∆х и выражает среднюю скорость изменения функции. , когда ∆х→0,при условии, что этот предел существует, называется производной функции:
, когда ∆х→0,при условии, что этот предел существует, называется производной функции:
 .
.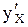 – (игрек штрих по икс); f ' (х) – (эф штрих по икс);
– (игрек штрих по икс); f ' (х) – (эф штрих по икс);  y' – (игрек штрих); dy/dх – (дэ игрек по дэ икс);
y' – (игрек штрих); dy/dх – (дэ игрек по дэ икс);  - (игрек с точкой).
- (игрек с точкой). Производная функции у = f(х)имеет простой геометрический смысл, связанный с понятием касательной к кривой линии в некоторой точке M. При этом, касательную, т.е. прямую линию аналитически выражают в виде у = кх = tg a· х, где a – угол наклона касательной (прямой) к оси Х. Представим непрерывную кривую как функцию у= f(х), возьмем на кривой точку M и близкую к ней точку М1и приведем через них секущую. Ее угловой коэффициент ксек=tg β =
Производная функции у = f(х)имеет простой геометрический смысл, связанный с понятием касательной к кривой линии в некоторой точке M. При этом, касательную, т.е. прямую линию аналитически выражают в виде у = кх = tg a· х, где a – угол наклона касательной (прямой) к оси Х. Представим непрерывную кривую как функцию у= f(х), возьмем на кривой точку M и близкую к ней точку М1и приведем через них секущую. Ее угловой коэффициент ксек=tg β = 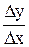 .Если приближать точку М1 к M, то приращение аргумента ∆хбудет стремиться к нулю, а секущая при β=α займет положение касательной. Из рис.2 следует: tgα =
.Если приближать точку М1 к M, то приращение аргумента ∆хбудет стремиться к нулю, а секущая при β=α займет положение касательной. Из рис.2 следует: tgα =  tgβ =
tgβ =  =у'x. Но tgαравен угловому коэффициенту касательной к графику функции:
=у'x. Но tgαравен угловому коэффициенту касательной к графику функции: х и находят приращенное значение функции в точке (х + ∆х), равное
х и находят приращенное значение функции в точке (х + ∆х), равное ;
; 
 = 2х+
= 2х+ 
 =
=  ;
; а ср =
а ср =  = f ' (х) = const.
= f ' (х) = const. =
=  или S=f(а,в); V=f(а,в,c); P=f (T,V).
или S=f(а,в); V=f(а,в,c); P=f (T,V). =
=  , если он существует. Частные производные по аргументам х и у обозначаются следующим образом: z'х; z'у; fх(х,у); fу(х,у);
, если он существует. Частные производные по аргументам х и у обозначаются следующим образом: z'х; z'у; fх(х,у); fу(х,у);  ;
;  ;
;  ;
;  . Частные производные I-го порядка функции z=f(х,у) также являются функциями аргументов хи у. Частные производные этих функций называются частными производными второго порядка искомой функции z=f(х,у). Для этой функции можно определить четыре частные производные 2-го порядка:
. Частные производные I-го порядка функции z=f(х,у) также являются функциями аргументов хи у. Частные производные этих функций называются частными производными второго порядка искомой функции z=f(х,у). Для этой функции можно определить четыре частные производные 2-го порядка: =
=  ;
;  =
=  ;
;  =
=  ;
;  . Частные производные
. Частные производные  отличаются порядком дифференцирования и называются смешанными частными производными второго порядка.
отличаются порядком дифференцирования и называются смешанными частными производными второго порядка. dy.
dy. при расчете погрешности измерения называется её абсолютной ошибкой. Если заменить полное приращение функции дифференциалом, то её абсолютная ошибка рассчитывается по приведенной формуле полного дифференциала.
при расчете погрешности измерения называется её абсолютной ошибкой. Если заменить полное приращение функции дифференциалом, то её абсолютная ошибка рассчитывается по приведенной формуле полного дифференциала. +
+  , где dR = ∆R, а dh = ∆h.
, где dR = ∆R, а dh = ∆h.


