ГИДРОДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ.
1. Стационарное течение жидкости. Условие неразрывности струи. Гидродинамика - раздел физики, в котором изучают вопросы движения жидкостей (несжимаемых) и взаимодействие их при этом с окружающими твердыми телами. К жидкостям относятся вещества, которые по своим свойствам занимают промежуточное положение между газами и твердыми телами. Жидкие среды составляют наибольшую часть организма, их перемещение обеспечивает обмен веществ и снабжение клеток кислородом, поэтому механические свойства и течение жидкостей представляют собой интерес для медиков и биологов. Рассмотрим установившееся или стационарное течение жидкости, т.е. такое течение, при котором скорости частиц жидкости в каждой точке потока со временем не изменяются.
Выделим трубку тока настолько узкую, что скорости частиц J в любом ее сечении S, перпендикулярном оси трубки, можно считать одинаковыми по всему сечению. Так как скорость частиц направлена вдоль линии тока, то частицы жидкости не могут выходить за пределы этой трубки. Тогда объем D V несжимаемой жидкости, протекающий через любое сечение трубки в единицу времени, остается постоянным: DV = J Соотношение (1) выражает условие неразрывности струи, т.к. только при сплошном течении через любое сечение за одно и то же время проходят одинаковые объемы несжимаемой жидкости. Тогда: J1S1 = J2S2 (рис.1), откуда Из условия неразрывности струи следует, что и для реальной жидкости при установившемся течении по трубе переменного сечения количество жидкости, протекающее за одно и то же время через любое сечение трубы, остается постоянным: Q = const. В частности, это с достаточно большой точностью выполняется и для кровотока в крупных кровеносных сосудах человека за время, равное нескольким, скажем трем, сердечным циклам, непосредственно следующих друг за другом. 2. Уравнение Бернулли и его следствия. Одно из наиболее важных уравнений, используемых для описания движущихся жидкостей, было впервые получено швейцарским математиком и физиком Даниилом Бернулли (1700-1782 г.г.). Для вывода уравнения Бернулли предположил, что имеем дело с идеальной жидкостью. Это значит, что мы пренебрегаем любыми силами вязкого сопротивления и трения. Пусть жидкость течет совершенно плавно без каких-либо турбулентностей, т.е. течение жидкости стационарное. Более того, мы рассматриваем только несжимаемые жидкости, так что определенная масса жидкости будет занимать одинаковый объем, несмотря на положение или условия в потоке.
Записывая каждую силу как произведение давления на площадь поперечного сечения, имеем: A = F1l1 – F2l2 = p1S1l1 – p2 S2l2 = (p1 – p2)DV, (3) где DV = DV1 = S1l1= S2l2 = DV2. Масса rDV жидкости под давлением p1, двигаясь с постоянной скоростью J1 на высоте h1, преобразуется в равную массу жидкости под давлением p2, движущуюся со скоростью J2 на высоте h2. Тогда изменения в потенциальной и кинетической энергиях между положениями 1 и 2 равны: DЕn = D(mgh) = mg Dh = rDVg(h2 – h1), (4а) DЕк = D( где мы выразили массу каждого объема жидкости как m =rΔV. Подставляя (3), (4а) и (4б) в (2), находим: (р1-р2) DV = rDVg(h2-h1) + Наконец, разделив на DV и перегруппировав члены, получаем: р1+rgh1+ Поскольку положения 1 и 2 произвольны, величина p+rgh+ p+rgh+ Это и есть уравнение Бернулли, которое может быть отнесено не только к сечениям трубки, но и к точкам, расположенным вдоль некоторой линии тока. Слагаемые, входящие в уравнение Бернулли, имеют размерность и смысл давления. Давление p называют статическим: оно не связано с движением жидкости и может быть измерено, например, манометром, перемещающимся вместе с жидкостью. Давление Для горизонтальной трубки тока гидростатическое давление остается постоянным (т.к. h = const) и может быть отнесено в правую часть уравнения (5), которое в этом случае можно записать так: рст+рдин=const. Статическое давление обуславливает потенциальную энергию жидкости (энергия давления), динамическое давление – кинетическую. Из последнего уравнения следует вывод, называемый правилом Бернулли: статическое давление невязкой жидкости при течении по горизонтальной трубке возрастает там, где скорость ее уменьшается и наоборот. Уравнение Бернулли, полученное для идеального случая, можно использовать и для объяснения реальных примеров.
3. Вязкость жидкости. Уравнение Ньютона. В реальной жидкости между молекулами действуют силы взаимного притяжения, обуславливающие внутреннее трение, или вязкость. Внутреннее трение, например, вызывает силу сопротивления при помешивании жидкости, замедляет скорости падения брошенных в неё тел. Ньютон установил, что сила Fтр внутреннего трения между двумя слоями жидкости, движущимися с различными скоростями, прямопропорциональна площади S соприкасающихся слоёв и градиенту скорости
где h - коэффициент пропорциональности, называемый коэффициентом внутреннего трения или динамической вязкостью (или просто вязкостью). Вязкость зависит от состояния и молекулярных свойств жидкости. Уравнение (6) – это уравнение Ньютона. Единицей вязкости в СИ является На практике вязкость жидкости характеризуют относительной вязкостью, под которой понимают отношение коэффициента вязкости η данной жидкости к коэффициенту вязкости воды ηв при той же температуре:
В большинстве жидкостей (вода, низкомолекулярные органические соединения, истинные растворы, расплавленные металлы и их соли) коэффициент вязкости зависит только от природы жидкости и температуры (с повышением температуры h понижается). Такие жидкости называются ньютоновскими. У некоторых жидкостей, преимущественно высокомолекулярных (растворы полимеров) или представляющих дисперсионные системы (суспензии, эмульсии), коэффициент вязкости зависит также от режима течения (давления и градиента скорости). При их увеличении вязкость жидкости уменьшается вследствие нарушения внутренней структуры потока жидкости. Такие жидкости называют структурно-вязкими или неньютоновскими. Их вязкость характеризуют так называемым условным коэффициентом вязкости, который относится к определённым условиям течения жидкости (давление, скорость). Кровь представляет собой суспензию форменных элементов в белковом растворе – плазме. Поэтому, строго говоря, она должна быть отнесена к неньютоновским жидкостям. Кроме того, при течении крови по сосудам наблюдается концентрация форменных элементов в центральной части потока, где вязкость соответственно увеличивается. Но так как вязкость крови не очень велика, этими явлениями часто пренебрегают и считают её коэффициент вязкости постоянной величиной. Относительная вязкость крови в норме составляет 4,2–6. При заболеваниях она может снижаться до 2–3 или повышаться до 15–20.
4. Ламинарное и турбулентное течение. Число Рейнольдса.
Простейшим типом движения жидкости является ламинарное течение, в котором слои потока постепенно сменяют друг друга. При низких скоростях течение потока через трубу будет ламинарным. Но при большой скорости ламинарное течение не может быть сохранено. Течение становится очень неравномерным, в потоке развиваются случайные вихри, и резко возрастает сопротивление. Этот тип движения называется турбулентным. Для турбулентного течения характерны местные изменения давления в жидкости, вызывающие колебательное движение ее частиц, которое сопровождается звуковыми явлениями (шум, журчание), благодаря которым турбулентное течение легко обнаруживается. Эксперименты показывают, что турбулентность возникает, когда определенная комбинация величин превосходит критическое значение. Эта комбинация называется числом Рейнольдса:
где r и h - соответственно плотность и вязкость жидкости, r - радиусы трубы, J - средняя скорость поступательного течения жидкости. Легко проверить, что Re - безразмерная величина. Поток через трубу будет ламинарным, если Re меньше 2000. Для Re > 3000 - поток турбулентный. Режим с Re между 2000 и 3000 является промежуточным, в котором течение не стабильно и может изменяться случайным образом между ламинарным и турбулентным. Поток крови в аорте в состоянии покоя является ламинарным и может быть выражен как произведение площади поперечного сечения аорты S и средней скорости потока, т.е.: Однако во время напряженной деятельности скорость 5. Течение вязкой жидкости по трубам. Формула Пуазейля. Гидравлическое сопротивление.
Течение вязкой жидкости по трубам представляет для медиков особый интерес, т.к. кровеносная система состоит в основном из цилиндрических сосудов разного диаметра. Вследствие симметрии ясно, что в трубе частицы текущей жидкости, равноудаленные от её оси, имеют одинаковую скорость. Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы, а самый близкий к трубе слой жидкости неподвижен. Примерное распределение скорости частиц жидкости в сечении трубы показано на рис. 4. Выделим мысленно цилиндрический объем жидкости некоторого радиуса r и длины l (см. рис.5а) и определим зависимость J=f (r). На торцах выделенного нами цилиндра поддерживаются давления p1 и p2 соответственно, что обуславливает результирующую силу: F=p1pr2 - p2pr2 = (p1-p2)pr2. На боковую поверхность цилиндра со стороны окружающего слоя жидкости действует сила внутреннего трения, равная в данном случае:
где S = 2prl - площадь боковой поверхности цилиндра. Так как жидкость движется равномерно, то силы, действующие на выделенный цилиндр, уравновешены: F=Fтр. . Подставляя в это равенство выражение для F и Fтр и учитывая, что скорость уменьшается с увеличением r, т.е.
Следовательно, имеем: dJ = - Проинтегрируем это уравнение:
Здесь нижние пределы соответствуют слою, прилегающему к внутренней поверхности трубы (J = 0 при r = R), а верхние пределы – переменные. В результате интегрирования получаем параболическую зависимость скорости слоев жидкости от расстояния их до оси трубы (см. огибающую концов векторов скорости на рис.4)
Из этого выражения видно, что наибольшую скорость имеет слой, текущий вдоль оси трубы (r = 0):
а для пристеночного слоя (r = R) скорость равна “0”. Установим от каких факторов зависит объем Q жидкости, протекающей через горизонтальную трубу за 1 секунду. Для этого выделим цилиндрический слой радиусом r и толщиной dr(см. рис. 5б). Площадь сечения этого слоя dS=2prdr, т.к. слой тонкий, то можно считать, что он перемещается с одинаковой скоростью J. За 1с через слой переносится объем жидкости: dQ=JdS=J2prdr. (10) Подставляя (8) в (10), получаем:
или
Эта зависимость известна под названием формулы Пуазейля или Гагена-Пуазейля. Этой формуле можно придать и такой вид:
Величину Z называют гидравлическим сопротивлением. Оно обратно пропорционально четвертой степени радиуса и поэтому значительно возрастает с уменьшением радиуса трубы. Заметим, что если R удваивается, то Q возрастает в 16 раз. Аналогично, при уменьшении R поток значительно уменьшится. Так, если что-либо приведет к утомлению артериальных стенок (что вызывает уменьшение R), ослабевший поток крови может вызвать стенокардию, которая характеризуется болями в груди, сопровождающимися общим недомоганием. Улучшения состояния можно достичь, приняв некоторые вещества, например, нитроглицерин, который расслабляет мышцы артериальных стенок, увеличивает R и, соответственно, увеличивает поток крови и уменьшает нагрузку на сердце.
ЛЕКЦИЯ №9
|

 Стационарное течение характеризуют линиями тока - воображаемыми линиями, совпадающими с траекториями частиц. Касательные к линиям тока показывают направление вектора скорости частиц жидкости, густота этих графически изображенных линий пропорциональна скорости. Часть потока жидкости, ограниченная со всех сторон линиями тока, образует трубку тока или струю (рис. 1).
Стационарное течение характеризуют линиями тока - воображаемыми линиями, совпадающими с траекториями частиц. Касательные к линиям тока показывают направление вектора скорости частиц жидкости, густота этих графически изображенных линий пропорциональна скорости. Часть потока жидкости, ограниченная со всех сторон линиями тока, образует трубку тока или струю (рис. 1). = const. (1)
= const. (1) , т.е. средние скорости течения в различных сечениях трубы обратно пропорциональны площадям этих сечений.
, т.е. средние скорости течения в различных сечениях трубы обратно пропорциональны площадям этих сечений. Уравнение Бернулли можно вывести, используя закон сохранения энергии при протекании жидкости через трубу. Как показано на рис.2, трубка тока имеет различные площади поперечного сечения и различную высоту над некоторым исходным уровнем. Если совершить некоторую работу А над жидкостью, это вызовет изменение потенциальной и кинетической энергии жидкости: А = D Еп + D Ек (2). Выделим в трубке тока достаточно малый объем жидкости DV массой m. Мы совершаем работу, действуя силой F1 на количество жидкости в положении 1(рис.2) и перемещая каждый малый элемент этого объема на величину единичного перемещения l1 с постоянной скоростью J1. Так, объем DV1 =l1S1 перемещен на расстояние l1 и проделанная над жидкостью работа равна F1l1. Каково влияние этого перемещения на жидкость, находящуюся в положении 2? Поскольку жидкость несжимаема, перемещение объема l1S1 на расстояние l1 в положении 1 означает перемещение равного объема в положении 2. Поэтому количество жидкости с площадью поперечного сечения S2 смещается на расстояние l2 c постоянной скоростью J2, где S1l1 = S2l2. Объем жидкости в положении 2 движется вдоль трубы, толкая следующие слои жидкости. Сила F2 действует на объём при перемещении l2, поэтому работа, совершаемая этим объемом жидкости, равна F2l2. Результирующая работа сил, оказывающих давление p1 и p2 на торцы объемов 1 и 2 при их перемещении - А = F1l1 – F2l2, т.к. силы со стороны соседних трубок тока нормальны к поверхности рассматриваемой трубки тока (идеальная жидкость), то они работы не совершают.
Уравнение Бернулли можно вывести, используя закон сохранения энергии при протекании жидкости через трубу. Как показано на рис.2, трубка тока имеет различные площади поперечного сечения и различную высоту над некоторым исходным уровнем. Если совершить некоторую работу А над жидкостью, это вызовет изменение потенциальной и кинетической энергии жидкости: А = D Еп + D Ек (2). Выделим в трубке тока достаточно малый объем жидкости DV массой m. Мы совершаем работу, действуя силой F1 на количество жидкости в положении 1(рис.2) и перемещая каждый малый элемент этого объема на величину единичного перемещения l1 с постоянной скоростью J1. Так, объем DV1 =l1S1 перемещен на расстояние l1 и проделанная над жидкостью работа равна F1l1. Каково влияние этого перемещения на жидкость, находящуюся в положении 2? Поскольку жидкость несжимаема, перемещение объема l1S1 на расстояние l1 в положении 1 означает перемещение равного объема в положении 2. Поэтому количество жидкости с площадью поперечного сечения S2 смещается на расстояние l2 c постоянной скоростью J2, где S1l1 = S2l2. Объем жидкости в положении 2 движется вдоль трубы, толкая следующие слои жидкости. Сила F2 действует на объём при перемещении l2, поэтому работа, совершаемая этим объемом жидкости, равна F2l2. Результирующая работа сил, оказывающих давление p1 и p2 на торцы объемов 1 и 2 при их перемещении - А = F1l1 – F2l2, т.к. силы со стороны соседних трубок тока нормальны к поверхности рассматриваемой трубки тока (идеальная жидкость), то они работы не совершают. mJ2) =
mJ2) =  ), (4б)
), (4б) = p2+rgh2+
= p2+rgh2+  .
. На рис. 3 монометрические трубки 1 и 3 демонстрируют величину статического давления в разных сечениях горизонтальной трубки. Так как нижнее сечение этих трубок параллельно линиям тока, то динамического давления они не показывают. Оно определяется по разности между полным давлением pполн и статическим: pдин = pполн – pст . Для измерения полного давления используется трубка 2, изогнутая под прямым углом к потоку (рис.3). Здесь S2<S1, J2>J1 и p2<p1. Сечение трубки S2 можно сделать столь узким, что вследствие малого статического давления (ниже атмосферного) в это сечение будет засасываться воздух или жидкость (всасывающее действие струи). Это используется в водоструйных насосах, медицинских ингаляторах, в пульверизаторах.
На рис. 3 монометрические трубки 1 и 3 демонстрируют величину статического давления в разных сечениях горизонтальной трубки. Так как нижнее сечение этих трубок параллельно линиям тока, то динамического давления они не показывают. Оно определяется по разности между полным давлением pполн и статическим: pдин = pполн – pст . Для измерения полного давления используется трубка 2, изогнутая под прямым углом к потоку (рис.3). Здесь S2<S1, J2>J1 и p2<p1. Сечение трубки S2 можно сделать столь узким, что вследствие малого статического давления (ниже атмосферного) в это сечение будет засасываться воздух или жидкость (всасывающее действие струи). Это используется в водоструйных насосах, медицинских ингаляторах, в пульверизаторах. между ними (градиент скорости между слоями – это изменение скорости, отнесённое к длине в направлении, перпендикулярном скорости):
между ними (градиент скорости между слоями – это изменение скорости, отнесённое к длине в направлении, перпендикулярном скорости): , (6)
, (6) , в системе СГС –
, в системе СГС –  , эта единица называется пуазом (П). Соотношение между ними: 1Па . с =10П.
, эта единица называется пуазом (П). Соотношение между ними: 1Па . с =10П. .
. , (7)
, (7) .
. расхода крови растет, а это приводит к тому, что число Re достигает 2000 и течение становится турбулентным. В мелких кровеносных сосудах скорость остается достаточно малой и поток по-прежнему ламинарный.
расхода крови растет, а это приводит к тому, что число Re достигает 2000 и течение становится турбулентным. В мелких кровеносных сосудах скорость остается достаточно малой и поток по-прежнему ламинарный.
 ,
, (значит и Fтр надо взять со знаком «минус»), получаем:
(значит и Fтр надо взять со знаком «минус»), получаем: .
. .
. .
. . (8)
. (8) , (9)
, (9) откуда интегрированием по всему сечению находим:
откуда интегрированием по всему сечению находим:
 ,
, ;
; 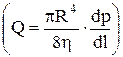 . (11)
. (11) , где
, где  . (12)
. (12)


