МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
1. Понятие о колебательном движении. Гармонические колебания.
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Колебательное движение и вызываемые им волны очень часто встречаются в природе и технике. Колеблются мосты под действием проходящих по ним поездов, совершает колебания барабанная перепонка уха, вибрируют части зданий, ритмично сокращается сердечная мышца.
Рассмотрим простейшую механическую систему, состоящую из тела (шар) некоторой массы m, нанизанного на стержень, и пружины с жёсткостью k, соединяющей его с неподвижной стеной. Направим ось OX вдоль стержня, а начало координат совместим с центром шара, при условии, что пружина находится в недеформированном состоянии. Сместим шар на расстояние X0 от положения равновесия (см. рис.1). Тогда со стороны пружины на тело будет действовать упругая сила F=-kX0 (1). Эта сила, как видно из уравнения (1), пропорциональна смещению и направлена в сторону противоположную смещению. Её называют возвращающей силой. Кроме того, система будет обладать запасом потенциальной энергии
2. Незатухающие гармонические колебания.
Пусть на тело массой m действует сила, стремящаяся вернуть его в положение равновесия (возвращающая сила) и пропорциональная смещению от положения равновесия, т.е. сила упругости FУПР= -kX. Если трение отсутствует, тогда уравнение второго закона Ньютона для тела имеет вид:
Обозначим Уравнение (1) является линейным однородным дифференциальным уравнением 2-го порядка, с постоянными коэффициентами. Решение уравнения (1) будет законом свободных или собственных незатухающих колебаний:
где A – величина наибольшего отклонения от положения равновесия, которая называется амплитудой (амплитуда – постоянная, положительная величина);
Т – период колебания (промежуток времени одного полного колебания); Чтобы найти скорость материальной точки при гармоническом колебании, нужно взять производную от выражения для смещения:
где
где 3. Затухающие гармонические колебания.
В реальных условиях, кроме возвращающей силы в колеблющейся системе будет действовать сила трения (сила сопротивления среды), которая при небольших скоростях пропорциональна скорости движения тела: Из уравнения видно, что амплитуда
Графически затухающие колебания представлены на рис.3.
С ростом коэффициента затухания, период колебаний увеличивается и при
Для характеристики скорости затухания колебаний вводится понятие коэффициента затухания
откуда βτ=1, следовательно
4. Энергия колебательного движения. В общем виде кинетическая энергия выражается формулой:
Потенциальную энергию колебательного движения найдём, исходя из общей формулы для потенциальной энергии при упругой деформации Складывая кинетическую и потенциальную энергии, получим полную механическую энергию колеблющейся материальной точки:
Графическая зависимость кинетической, потенциальной и полной энергии колеблющейся системы от времени показана на рис.5.
5. Вынужденные колебания.
Свободное колебательное движение механической системы всегда является затухающим в силу наличия трения. Для того,чтобы система совершала незатухающие колебания, необходимо восполнить извне потери энергии на трение. Для этого необходимо воздействовать на систему внешней периодически изменяющейся силой:
где
Из формулы смещения видно: 1) установившиеся вынужденные колебания, происходящие под воздействием гармонически изменяющейся вынуждающей силы, также являются гармоническими; 2) частота вынужденного колебания совпадает с частотой вынуждающей силы; 3) вынужденные колебания сдвинуты по фазе относительно вынуждающей силы. Из выражения для амплитуды следует, что она прямопропорциональна амплитуде вынуждающей силы и имеет сложную зависимость от β, ω0, ωВ. Если ω0 и β вполне определённые величины, то амплитуда вынужденных колебаний имеет максимальное значение при некоторой определённой частоте вынуждающей силы. Явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колеблющегося тела называется резонансом. Происходящие при этом колебания – резонансными, а их частота ωрез – резонансной частотой колебаний. Резонансную круговую частоту можно найти, если найти максимум знаменателя в выражении для амплитуды:
Резонанс в одних случаях бывает полезным, т.к. при этом действием незначительной возбуждающей силы можно вызвать колебания с относительно большой амплитудой. Вредное действие резонанса связано с разрушениями, которые он может вызвать. Отдельные органы человека имеют также собственную частоту. Если бы коэффициент затухания внутренних органов был невелик, то резонансные явления, возникшие в этих органах под воздействием внешней вибрации или звуковых колебаний, могли бы привести к нежелательным явлениям, обусловленным повреждением этих органов. Однако, такие явления при умеренных внешних воздействиях практически не наблюдаются, т.к. β биологических систем является большим по величине. И тем не менее резонансные явления при действии внешних механических колебаний имеют место в биологических системах. В этом, очевидно, заключается одна из причин отрицательного воздействия инфразвуковых колебаний и вибрации на организм человека. Например, резонансные колебания головы человека при частотах 8-27 Гц могут стать причиной уменьшения остроты зрения. 6. Сложение гармонических колебаний одинакового направления.
Возможны случаи, когда тело участвует одновременно в нескольких колебаниях. Например, различные звуковые волны, одновременно воспринимаемые нашим ухом, заставляют барабанную перепонку принимать участие сразу в нескольких гармонических колебаниях (слышать голоса многих людей). Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты. Смещение X колеблющегося тела будет являться суммой смещений X1 и X2, которые запишутся следующим образом:
Смещение результирующего колебания можно получить, сложив эти выражения и произведя соответствующие тригонометрические преобразования. Но мы воспользуемся методом векторных диаграмм, который отличается большей простотой и наглядностью. Суть метода состоит в том, что: 1) синусоидальная (косинусоидальная) величина изображается вращающимся вектором, длина которого в выбранном масштабе выражает амплитуду синусоиды; 2) угол, образованный вектором с положительным направлением оси абсцисс в начальный момент времени равен начальной фазе; 3) скорость вращения вектора равна угловой частоте; 4)
мгновенные значения синусоидальной (косинусоидальной) величины выражаются проекциями вращающегося вектора на оси координат (рис.7). Представим оба колебания с помощью векторов A1 и A2. Построим по правилам сложения векторов результирующий вектор A. Легко видеть, что проекция этого вектора на ось X равна сумме проекций слагаемых векторов
Анализируя первое выражение, приходим к выводам: а) если разность фаз обоих колебаний б) если разность фаз Если частота колебаний X1 и X2 неодинаковы, то A1 и A2 будут вращаться с различными скоростями. В этом случае результирующий вектор A пульсирует по величине и вращается с непостоянной скоростью. Следовательно, результирующее движение будет не гармоническим колебанием, а представлять некоторый сложный колебательный процесс. 7. Сложное колебание и его гармонический спектр.
Колебательное движение, при котором смещение изменяется во времени по любому закону, кроме гармонического, называется сложным колебанием. Любое сложное колебание может быть представлено как сумма простых колебаний, что значительно упрощает его анализ. Разложение сложного колебания часто диктуется необходимостью практики. Этот вопрос в общем виде был решён математиком Фурье, который показал, что периодическая функция любой сложности может быть представлена в виде суммы простых гармонических колебаний, частоты которых кратны частоте сложной периодической функции. Совокупность простых колебаний, на которые можно разложить данное сложное колебание, называют гармоническим спектром. Такое разложение негармонической функции на гармонические колебания называется гармоническим частотным анализом. Разложение сложного колебания на составляющие его простые гармонические колебания выполняется чаще всего на основе его графика, причём для анализа применяются специальные приборы, называемые гармоническими анализаторами. Подобные приборы применяются при специальных исследованиях колебательных процессов в медицине, например, записанных на ленте колебаний биопотенциалов мозга. Такое разложение биопотенциалов мозга может быть использовано с диагностической целью.
В спектре сложного колебания указываются частоты и амплитуды всех составляющих его простых колебаний. Обычно спектр изображается в виде графика: (рис.9б), на горизонтальной оси которого откладываются частоты, причём у каждой частоты (гармоники) простого колебания строится ордината, соответствующая амплитуде этого колебания. На рисунке 9а приведён график сложного колебания и 3 его гармоники с частотами 1 Гц, 3 Гц и 5 Гц. Гармонический спектр сложного колебания в данном случае называют линейчатым. Гармонический анализ позволяет достаточно детально проанализировать и описать любой сложный колебательный процесс. Он находит применение в акустике, радиотехнике и других областях науки и техники. ЛЕКЦИЯ №6
|

 В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные и др.. Мы рассмотрим механические колебания.
В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные и др.. Мы рассмотрим механические колебания. . Если отпустить груз, то под действием упругой силы он станет двигаться к положению равновесия, при этом его потенциальная энергия будет уменьшаться, переходя в кинетическую
. Если отпустить груз, то под действием упругой силы он станет двигаться к положению равновесия, при этом его потенциальная энергия будет уменьшаться, переходя в кинетическую 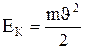 , возвращающая сила будет убывать и в положении равновесия станет равной нулю, но тело в положении равновесия не остановиться, а по инерции будет продолжать движение. Его кинетическая энергия будет переходить в потенциальную, возвращающая сила станет расти, но её направление изменится на противоположное. В системе возникнут колебания. При колебательном движении положение тела в каждый данный момент времени характеризуется расстоянием от положения равновесия, которое называется смещением. Среди различных видов колебаний наиболее простой формой является гармоническое колебание, т.е. такое, при котором колеблющаяся величина изменяется в зависимости от времени по закону синуса или косинуса.
, возвращающая сила будет убывать и в положении равновесия станет равной нулю, но тело в положении равновесия не остановиться, а по инерции будет продолжать движение. Его кинетическая энергия будет переходить в потенциальную, возвращающая сила станет расти, но её направление изменится на противоположное. В системе возникнут колебания. При колебательном движении положение тела в каждый данный момент времени характеризуется расстоянием от положения равновесия, которое называется смещением. Среди различных видов колебаний наиболее простой формой является гармоническое колебание, т.е. такое, при котором колеблющаяся величина изменяется в зависимости от времени по закону синуса или косинуса.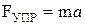 ;
;  или
или 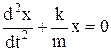 .
. , получим
, получим 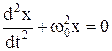 . (1)
. (1) ,
,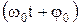 - фаза колебаний;
- фаза колебаний; 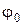 - начальная фаза.
- начальная фаза. Графически незатухающие колебания представлены на рис.2:
Графически незатухающие колебания представлены на рис.2: , где
, где 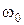 - круговая или циклическая частота,
- круговая или циклическая частота,  , ν называется частотой колебания.
, ν называется частотой колебания. ,
,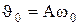 - максимальная скорость (амплитуда скорости). Продифференцировав это выражение, найдём ускорение:
- максимальная скорость (амплитуда скорости). Продифференцировав это выражение, найдём ускорение: ,
, - максимальное ускорение.
- максимальное ускорение. , где r – коэффициент сопротивления. Если ограничиться учётом возвращающей силы и силы трения, то уравнение движения примет вид:
, где r – коэффициент сопротивления. Если ограничиться учётом возвращающей силы и силы трения, то уравнение движения примет вид: 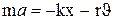 или
или 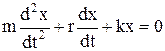 , разделив на m, получим:
, разделив на m, получим: 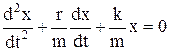 , обозначив
, обозначив  ,
,  . Это уравнение носит название линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Решение этого уравнения будет законом свободных затухающих колебаний, и будет иметь следующий вид:
. Это уравнение носит название линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Решение этого уравнения будет законом свободных затухающих колебаний, и будет иметь следующий вид: 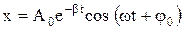 .
.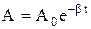 не является постоянной, а зависит от времени и убывает по экспоненциальному закону. Как и для незатухающих колебаний, величина ω – называется круговой частотой:
не является постоянной, а зависит от времени и убывает по экспоненциальному закону. Как и для незатухающих колебаний, величина ω – называется круговой частотой: 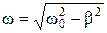 , где
, где 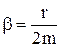 - коэффициент затухания;
- коэффициент затухания; Определим период колебаний
Определим период колебаний  или
или 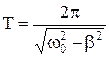 , откуда видно, что колебания в системе могут возникать только при условии если сопротивление незначительно
, откуда видно, что колебания в системе могут возникать только при условии если сопротивление незначительно 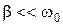 . Период колебаний практически равен
. Период колебаний практически равен 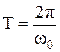 .
. обращается в бесконечность. Движение перестаёт быть периодическим. Выведенная из положения равновесия система возвращается в состояние равновесия, не совершая колебаний. Такое движение называется апериодическим.
обращается в бесконечность. Движение перестаёт быть периодическим. Выведенная из положения равновесия система возвращается в состояние равновесия, не совершая колебаний. Такое движение называется апериодическим. На рис.4 показан один из случаев возвращения системы в положение равновесия при апериодическом движении. В соответствии с указанной кривой спадает заряд на мембранах нервных волокон человека.
На рис.4 показан один из случаев возвращения системы в положение равновесия при апериодическом движении. В соответствии с указанной кривой спадает заряд на мембранах нервных волокон человека.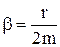 . Найдём время τ, за которое амплитуда колебаний уменьшится в e раз:
. Найдём время τ, за которое амплитуда колебаний уменьшится в e раз: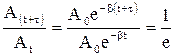 , т.е.
, т.е. 
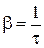 . Коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшится в e раз. Отношение значений амплитуд, соответствующих моментам времени, отличающихся на период, равное
. Коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшится в e раз. Отношение значений амплитуд, соответствующих моментам времени, отличающихся на период, равное 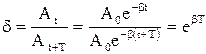 называют декрементом затухания, а его логарифм – логарифмическим декрементом затухания:
называют декрементом затухания, а его логарифм – логарифмическим декрементом затухания: .
.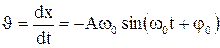 ,
, .
. . Тогда
. Тогда 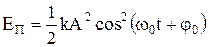 .
.
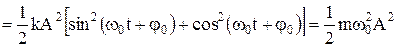 ,
, т.е. в отсутствии сил трения полная механическая энергия системы не изменяется (величины m, ω0, A – являются постоянными).
т.е. в отсутствии сил трения полная механическая энергия системы не изменяется (величины m, ω0, A – являются постоянными). . Внешняя сила, обеспечивающая незатухающие колебания, называется вынуждающей силой, а вынужденными колебаниями называются такие колебания, которые возникают в системе при участии внешней силы, изменяющейся по периодическому закону. Дифференциальное уравнение колебания будет иметь следующий вид:
. Внешняя сила, обеспечивающая незатухающие колебания, называется вынуждающей силой, а вынужденными колебаниями называются такие колебания, которые возникают в системе при участии внешней силы, изменяющейся по периодическому закону. Дифференциальное уравнение колебания будет иметь следующий вид: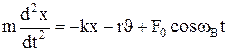 , или
, или  ,
, ; x – смещение материальной точки в установившихся вынужденных колебаниях:
; x – смещение материальной точки в установившихся вынужденных колебаниях:  , где
, где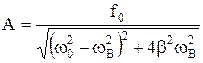 .
.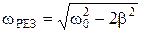 . Тогда, подставив это выражение в формулу для амплитуды вместо ωВ, получим:
. Тогда, подставив это выражение в формулу для амплитуды вместо ωВ, получим:  .
. Графически зависимость амплитуды A вынужденных колебаний от частоты вынуждающей силы при разных значениях коэффициента затухания показана на рис.6 (β1>β2>β3). Степень нарастания амплитуды, или острота кривой резонанса, зависит от коэффициента β, чем он меньше тем острее резонанс. При β=0, ωрез= ω0, т.е. резонанс в системе без затухания наступает, когда частота вынуждающей силы совпадает с частотой собственных колебаний.
Графически зависимость амплитуды A вынужденных колебаний от частоты вынуждающей силы при разных значениях коэффициента затухания показана на рис.6 (β1>β2>β3). Степень нарастания амплитуды, или острота кривой резонанса, зависит от коэффициента β, чем он меньше тем острее резонанс. При β=0, ωрез= ω0, т.е. резонанс в системе без затухания наступает, когда частота вынуждающей силы совпадает с частотой собственных колебаний.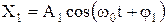 ,
, 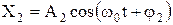 .
.

 , следовательно, вектор A представляет собой результирующее колебание (см. рис.8). Этот вектор вращается с той же угловой скоростью ω0 как и вектор A1 и A2, так что результирующее движение будет гармоническим колебанием с частотой ω0, амплитудой A и начальной фазой φ. Из построения видно, что
, следовательно, вектор A представляет собой результирующее колебание (см. рис.8). Этот вектор вращается с той же угловой скоростью ω0 как и вектор A1 и A2, так что результирующее движение будет гармоническим колебанием с частотой ω0, амплитудой A и начальной фазой φ. Из построения видно, что 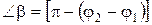 , тогда
, тогда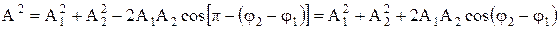
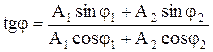 .
.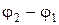 равна нулю, амплитуда результирующего колебания равна сумме амплитуде A1+A2;
равна нулю, амплитуда результирующего колебания равна сумме амплитуде A1+A2; , т.е. оба колебания находятся в противофазе, то амплитуда результирующего колебания равна (A1-A2).
, т.е. оба колебания находятся в противофазе, то амплитуда результирующего колебания равна (A1-A2).



