МЕХАНИЧЕСКИЕ ВОЛНЫ. АКУСТИКА.
1. Механические волны. Уравнение волны. Волновое уравнение.
Если какое-либо тело совершает колебания в упругой среде, то оно взаимодействует с частицами среды и заставляет их совершать вынужденные колебания. Постепенно всё более удалённые частицы вовлекаются в колебательное движение. Процесс распространения колебаний, или особых возмущений состояния вещества или поля в пространстве с течением времени называют волнами. Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны, и продольной, если колебания частиц среды происходят в направлении распространения волны. Упругие волны возникают благодаря связи, существующей между частицами среды: перемещение одной частицы от положения равновесия приводит к перемещению соседних частиц. Этот процесс распространяется в пространстве с определённой скоростью. Уравнение волны выражает зависимость смещения колеблющейся точки, участвующей в волновом процессе, от координаты её равновесного положения и времени. Для волны, распространяющейся вдоль оси OX в общем виде эта зависимость имеет вид: S = f(x,t). Выведем уравнение плоской волны. Если источник волн находится в точке с координатой X = 0 (точка А), рис.1, то уравнение колебаний определяется формулой:
или: Полученное соотношение и есть уравнение плоской волны, распространяющейся вдоль оси X. Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, возьмём вторые частные производные по координате и времени от уравнения плоской волны
Сопоставляя вторые производные, находим, что при умножении обеих частей уравнения (1) на Уравнение (3) и есть искомое волновое уравнение, т.к. оно получено из уравнения плоской волны, распространяющейся вдоль оси X и представляет частный случай более общего уравнения:
2. Энергия волны. Вектор Умова.
Чтобы подсчитать энергию, переносимую волной, выделим мысленно некоторую площадку S, расположенную перпендикулярно направлению распространения волны. Пусть в начальный момент времени (t=0), фронт плоской волны совпадает с этой площадкой. За время t>>T (где T – период) фронт волны переместится на расстояние
где Итак: Вектор 3. Эффект Доплера. Эффектом Доплера называют изменение частоты волн, воспринимаемых наблюдателем (приёмником волны) вследствие относительного движения источника волн и наблюдателя. При теоретическом рассмотрении явления следует отметить, что все скорости (скорость распространения колебаний, скорость наблюдателя и источника) отсчитываются относительно воздуха. Рассмотрим простейшие случаи, когда источник волн и наблюдатель движутся относительно среды вдоль одной прямой. Скорость распространения волн в среде будем считать равной
Второй случай – наблюдатель приближается со скоростью Эффект Доплера наблюдается в волновых движениях любого типа – в волнах на воде, звуковых, радио-, световых волнах. Например, доплеровский локатор специально используется дорожной милицией для определения автомобилей, водители которых превышают допустимую скорость движения.
4. Природа звука. Физические характеристики звуковых волн.
В узком смысле слова под “акустикой” понимают учение о звуке, т.е. об упругих колебаниях и волнах в различных средах, воспринимаемых ухом человека. Звуковые колебания – это частный случай механических колебаний, распространяющихся в пространстве в форме продольных волн. В связи с важностью акустических понятий для оценки слуховых ощущений, а так же в связи с рядом медицинских приложений данного раздела, остановимся на некоторых характеристиках звука, знание которых необходимо врачу, поскольку звук несёт около 15% информации об окружающем нас мире, а также может быть источником информации о состоянии внутренних органов человека. Источником звука являются тела (твёрдые, жидкие, газообразные), совершающие колебания в результате каких-либо механических воздействий. Колеблющееся тело излучает в окружающую среду, например, воздух, упругую продольную волну, которая, достигая уха, вызывает слуховые ощущения. Звуки разделяют: 1) Тоны или музыкальные звуки; 2) Шумы; 3) Звуковые удары. Тон – это звук, являющийся периодическим процессом с постоянной или закономерно изменяющейся во времени частотой. Если это гармонический процесс, то тон называется простым или чистым. Негармоническому колебанию соответствует сложный тон. Простой тон может быть получен с помощью камертона, звукового генератора. Сложный тон создаётся музыкальными инструментами, аппаратом речи. Сложный тон может быть разложен на простые. Наименьшая частота Шумом называют звук, отличающийся сложной, не повторяющейся во времени зависимостью (шорох, скрип, аплодисменты, звуки от вибрации машин). Звуковой удар – это кратковременное звуковое воздействие (хлопок, взрыв). Звуковой тон характеризуется частотой (периодом), амплитудой, гармоническим спектром, а также интенсивностью или силой звука и звуковым давлением. Интенсивностью или силой звука называют плотность потока энергии звуковой волны: Для плоской гармонической волны давление связано с интенсивностью звука соотношением: Ухо человека воспринимает широкий диапазон интенсивностей. Для того, чтобы волны звуковой частоты создали ощущение звука, необходимо, чтобы интенсивность превышала некоторую минимальную величину I0, называемую порогом слышимости. Например, на частоте Поскольку диапазон интенсивностей, воспринимаемых звуков довольно велик, оказывается удобным сравнивать интенсивности звука в логарифмической шкале. Шкала уровней интенсивности создаётся следующим образом: значение I0 принимается за начальный уровень, уровень интенсивности любого звука с интенсивностью I выражают через десятичный логарифм её отношения к I0: Если уровень интенсивности некоторого звука L=1Б, то отношение его интенсивности к I0 будет равно 10 (lg10=1), если же L=2Б, то I/I0=102 (lg102=2). Бел – это довольно большая единица, поэтому обычно уровень интенсивности выражают в децибелах: 1Б=10дБ, тогда
5. Распространение звуковых волн в среде. Волновое сопротивление.
Звук распространяется в любых средах, скорость его распространения не зависит от частоты колебаний, но зависит от упругости и плотности среды, а также от её температуры. В воздухе при t=0oC Как уже было сказано, интенсивность волны Приведём примеры усреднённых значений этого отношения для частоты 512 Гц: Окно открытое – 1; Стена кирпичная – 0,032; Войлок толщиной 2,5 см – 0,55. Мягкие ткани обладают большим поглощением, поэтому их применяют в тех случаях, когда желательно уменьшить отражение звука от стен. Рэлей показал, что коэффициент проникновения звука определяется формулой:
Наибольшее значение, которое может иметь коэффициент β, равно единице. Из (4) видно, что β=1, если Примеры волнового сопротивление некоторых веществ при 20оС: Воздух – 440 кг. м-2с-1; Бетон–4800000 кг. м-2с-1; Вода–1440000 кг. м-2с-1. Для бетона Вывод: только очень малая часть звуковой энергии проходит из воздуха в бетон. Такие расчёты могут быть использованы для оценки уровней интенсивности громких шумов и возможности звукоизоляции. Устранение источников вредных звуков или ослабление их действия с помощью звукопоглощающих материалов находится под контролем санитарной службы, так как шум оказывает вредное воздействие на здоровье человека. Нормально допустимый уровень интенсивности шума 40 – 50 дБ. Предельно допустимый уровень (для высоких частот) – 75 – 80 дБ и 90 – 100 дБ – для низкочастотных звуков. Для измерения уровня интенсивности шума используют специальные приборы – шумомеры. В них звуковые колебания преобразуются в электрические. Шкала электроизмерительного прибора шумомера непосредственно проградуирована в децибелах. Лекция №7
|

 .
. До точки B с некоторой координатой X возмущение дойдёт за время τ, поэтому колебание этой точки запаздывают:
До точки B с некоторой координатой X возмущение дойдёт за время τ, поэтому колебание этой точки запаздывают: или
или  , где
, где  - скорость распространения волны. При этом предполагается, что в процессе распространения волны не происходит её затухание. Время запаздывания может быть выражено:
- скорость распространения волны. При этом предполагается, что в процессе распространения волны не происходит её затухание. Время запаздывания может быть выражено:  , где
, где  - длина волны, тогда:
- длина волны, тогда: ;
; ,
,  .
. :
: ;
;  ; (1)
; (1) ;
;  . (2)
. (2) правые части уравнения (1) и (2) будут равны, а, значит, равны и левые:
правые части уравнения (1) и (2) будут равны, а, значит, равны и левые:  . (3)
. (3) .
. Волновой процесс в среде связан с распространением энергии колебаний.
Волновой процесс в среде связан с распространением энергии колебаний. , тогда в колебательный процесс будет вовлечена масса вещества
, тогда в колебательный процесс будет вовлечена масса вещества  . Полная энергия массы
. Полная энергия массы  . Энергия, переносимая волной в среде за единицу времени через единичную площадку, называется интенсивностью волны. Обозначим её буквой I тогда:
. Энергия, переносимая волной в среде за единицу времени через единичную площадку, называется интенсивностью волны. Обозначим её буквой I тогда: ,
,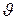 - скорость распространения волны.
- скорость распространения волны. , где
, где  - объёмная плотность энергии. Интенсивность волны измеряется в Вт/м2.
- объёмная плотность энергии. Интенсивность волны измеряется в Вт/м2. , показывающий направление распространения волн и равный потоку энергии волн, проходящему через единичную площадку, перпендикулярную этому направлению, называют вектором Умова:
, показывающий направление распространения волн и равный потоку энергии волн, проходящему через единичную площадку, перпендикулярную этому направлению, называют вектором Умова: 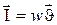 .
. ; скорость наблюдателя -
; скорость наблюдателя -  .
. Пусть наблюдатель неподвижен, а источник волн движется с постоянной скоростью
Пусть наблюдатель неподвижен, а источник волн движется с постоянной скоростью  <
<  , а частота
, а частота  . Поделив числитель и знаменатель на
. Поделив числитель и знаменатель на  , т.е. наблюдатель будет воспринимать звук с частотой большей, чем частота неподвижного источника. Если же источник движется от наблюдателя, то
, т.е. наблюдатель будет воспринимать звук с частотой большей, чем частота неподвижного источника. Если же источник движется от наблюдателя, то  будет меньше, т.е.
будет меньше, т.е.  .
. . Учитывая, что
. Учитывая, что  , получим
, получим  , т.е. наблюдатель воспринимает большую частоту колебаний, чем частота источника. Если же наблюдатель удаляется от источника
, т.е. наблюдатель воспринимает большую частоту колебаний, чем частота источника. Если же наблюдатель удаляется от источника  , то частота, воспринимаемая им, будет меньшей, т.е.
, то частота, воспринимаемая им, будет меньшей, т.е.  .
. Использование эффекта Доплера для определения скорости движущихся тел нашло применение в медицине. Рассмотрим следующую систему: генератор Уз волн совмещён с приёмником, частота генератора
Использование эффекта Доплера для определения скорости движущихся тел нашло применение в медицине. Рассмотрим следующую систему: генератор Уз волн совмещён с приёмником, частота генератора  . В среде со скоростью
. В среде со скоростью  движется объект. Скорость распространения ультразвука -
движется объект. Скорость распространения ультразвука -  . Разница частот будет равна
. Разница частот будет равна  и называется доплеровским сдвигом. В медицинских приложениях скорость Уз больше скорости движущегося объекта
и называется доплеровским сдвигом. В медицинских приложениях скорость Уз больше скорости движущегося объекта  . Для этого случая
. Для этого случая  . Эффект Доплера используется для определения скорости кровотока, скорости движения клапанов и стенок сердца (доплеровская эхокардиография) и других органов.
. Эффект Доплера используется для определения скорости кровотока, скорости движения клапанов и стенок сердца (доплеровская эхокардиография) и других органов. такого разложения соответствует основному тону. Остальные гармоники (обертона) имеют частоты
такого разложения соответствует основному тону. Остальные гармоники (обертона) имеют частоты  ,
,  , … Набор частот с указанием их относительной интенсивности (амплитуды) называют акустическим спектром, являющимся важной физической характеристикой сложного тона.
, … Набор частот с указанием их относительной интенсивности (амплитуды) называют акустическим спектром, являющимся важной физической характеристикой сложного тона. . Звуковое давление – это дополнительное давление р, которое возникает в среде при прохождении звуковых волн. Звуковое давление измеряется в Н/м2.
. Звуковое давление – это дополнительное давление р, которое возникает в среде при прохождении звуковых волн. Звуковое давление измеряется в Н/м2. , где р0 – амплитудное значение; рЭФ – эффективное значение давления.
, где р0 – амплитудное значение; рЭФ – эффективное значение давления. I0=10-12 Вт/м2 или р0=2.10-5 Па. С другой стороны, звуки очень большой интенсивности не воспринимаются как звук, вызывая лишь ощущение боли в ухе. Максимальная величина интенсивности, при превышении которой возникает ощущение боли, называется порогом болевого ощущения: Imax=10 Вт/м2 или рmax=60 Па для частоты
I0=10-12 Вт/м2 или р0=2.10-5 Па. С другой стороны, звуки очень большой интенсивности не воспринимаются как звук, вызывая лишь ощущение боли в ухе. Максимальная величина интенсивности, при превышении которой возникает ощущение боли, называется порогом болевого ощущения: Imax=10 Вт/м2 или рmax=60 Па для частоты  .
. . В этой шкале уровень интенсивности выражают в белах (Б). Бел – единица, получившая своё название в честь изобретателя телефона Александра Грейама Белла (1847-1922 г.г.).
. В этой шкале уровень интенсивности выражают в белах (Б). Бел – единица, получившая своё название в честь изобретателя телефона Александра Грейама Белла (1847-1922 г.г.).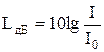 или
или  . Порог слышимости I0 имеет уровень интенсивности L=0дБ, а болевой порог – 130дБ.
. Порог слышимости I0 имеет уровень интенсивности L=0дБ, а болевой порог – 130дБ. . С ростом температуры скорость увеличивается. В твёрдых и жидких средах скорость звука больше. Для воды она равна 1500 м/с. Эта скорость соответствует примерно средней скорости в мягких тканях человека. Звуковая волна, встречая на своём пути тела, возбуждает в них колебания. При попадании на тело часть энергии отражается и преломляется (законы отражения и преломления звуковых волн аналогичны законам для света), часть энергии может поглотиться телом (поглощение может быть полным). Определённая часть энергии может выйти из тела. Таким образом, энергию волны можно разделить на отражённую, поглощённую, а также прошедшую через среду.
. С ростом температуры скорость увеличивается. В твёрдых и жидких средах скорость звука больше. Для воды она равна 1500 м/с. Эта скорость соответствует примерно средней скорости в мягких тканях человека. Звуковая волна, встречая на своём пути тела, возбуждает в них колебания. При попадании на тело часть энергии отражается и преломляется (законы отражения и преломления звуковых волн аналогичны законам для света), часть энергии может поглотиться телом (поглощение может быть полным). Определённая часть энергии может выйти из тела. Таким образом, энергию волны можно разделить на отражённую, поглощённую, а также прошедшую через среду. определяется звуковым амплитудным давлением и произведением
определяется звуковым амплитудным давлением и произведением  , которое называется волновым сопротивлением. Волновое сопротивление – важнейшая характеристика среды, определяющая условие отражения и преломления волн на её границе. Допустим, что плоская волна падает нормально к границе раздела двух сред, интенсивность её в первой среде – I1, интенсивность прошедшей волны во второй среде I2. Отношение
, которое называется волновым сопротивлением. Волновое сопротивление – важнейшая характеристика среды, определяющая условие отражения и преломления волн на её границе. Допустим, что плоская волна падает нормально к границе раздела двух сред, интенсивность её в первой среде – I1, интенсивность прошедшей волны во второй среде I2. Отношение  (1) называется коэффициентом проникновения звуковой волны. Это отношение (b) зависит от ряда факторов, в том числе и от частоты колебаний звуковой волны.
(1) называется коэффициентом проникновения звуковой волны. Это отношение (b) зависит от ряда факторов, в том числе и от частоты колебаний звуковой волны.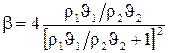 , где (4)
, где (4) - волновое сопротивление среды.
- волновое сопротивление среды. . Итак, при равенстве волновых сопротивлений двух сред звуковая волна пройдёт (при нормальном падении) границу раздела без отражения. Если волновое сопротивление второй среды значительно превышает волновое сопротивление первой, то
. Итак, при равенстве волновых сопротивлений двух сред звуковая волна пройдёт (при нормальном падении) границу раздела без отражения. Если волновое сопротивление второй среды значительно превышает волновое сопротивление первой, то  (так как
(так как  ).
). .
.


