ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
1. Неопределенный интеграл и его свойства. Многочисленные математические операции образуют пары двух взаимообратных действий. Например, сложение и вычитание, умножение и деление, возведение в целую степень и извлечение корня, логарифмирование и потенцирование. Дифференциальное исчисление решает следующую основную задачу: по данной функции найти ее производную. Обратным действием дифференцирования является интегрирование: для данной функции f(х) найти такую функцию F(х), производная которой равнялась бы заданной функции f(х), т.е. F'(х) = f(х) (1) Поставленную задачу можно сформулировать в следующей форме: для данной функции f(х) найти такую функцию F(х), дифференциал которой равнялся бы выражению f(х)d х: dF(х) = f(х)d х (2) Функция F(х), связанная с функцией f(х) соотношение (1) или (2), называется ее первообразной. Так, например, первообразной от функции f(х)= х 2 будет функция F(х)= х 3∕3, так как F'(х) = (х 3∕3)' = х 2 или то же самое dF = d(х 3∕3) = х 2 d х. В общем случае, если f(х) имеет первообразную функцию F(х), то совокупность [F(х)+С] также будет первообразной для нее, т.к. С' = 0 (С – постоянная величина). Следовательно, для данной функции f(х) может быть не одна, а множество первообразных [F(х)+С], отличающихся на некоторую постоянную интегрирования. Совокупность первообразных [F(х)+С] для данной функции f(х) или данного дифференциала f(х) d х. называют неопределенным интегралом от функции f(х) и обозначают ∫f(х)d х. По определению ∫;f(х)d х= [F(х)+С] (3) - читается «неопределенный интеграл эф от икс дэ икс», где f(х) d х – подинтегральное выражение; f(х) – подинтегральная функция; С – постоянная интегрирования; символ ∫ - знак неопределенного интеграла. Под знакомнеопределенного интеграла мы имеем не производную искомой функции, а ее дифференциал. Так как, например, функция F(х)= х 3∕3 является одной из первообразных от функции f(х)= х 2, то на основании формулы (3) получим ∫ х 2 d х = х 3∕3 + С. Рассмотрим основные свойства неопределенного интеграла: 1. Производная от неопределенного интеграла равна подинтегральной функции: [ ∫;f(х) d х ]' = [F(х) + С]' = F'(х) = f(х). 2. Дифференциал от неопределенного интеграла равен подинтегральному выражению: d[ ∫;f(х) d х ] = d[F(х) + С] = [F(х) + C]'d х = F'(х) d х= f(х) d х. 3. Интеграл от дифференциала первообразной равен самой первообразной: ∫d[F(х) + С] = ∫d F(х) = ∫f(х) d х = F(х + C). 4. Постоянный множитель можно выносить за знак неопределенного интеграла: ∫ к f(х) d х = к ∫f(х) d х. 5. Интеграл от алгебраической суммы равен алгебраической сумме интегралов слагаемых, т.е.: ∫;[f1(х) + f2(х) – f3(х)]d х = ∫;f1(х) d х + ∫;f2(х) d х - ∫;f3(х) d х. Пример: Найти ∫(х 3+3sin х –8)d х = ∫ х 3d х+ 3∫sin х d х- 8∫d х = х 4/4–3cos х –8 х +С. Используя формулы интегрирования для трех интегралов, при каждом интегрировании получим свою произвольную постоянную. Но в конечном итоге мы имеем только одну произвольную постоянную, так как, если С1; С2;С3 – произвольные постоянные, то и величина С равная их алгебраической сумме, также является произвольной постоянной.
2. Простейшие способы интегрирования. а) Непосредственное интегрирование. Нахождение интегралов функций, основанное на прямом применении свойств неопределенных интегралов и таблицы основных формул интегрирования. Рассмотрим пример нахождения интеграла функции путем непосредственного интегрирования. Пример: ∫(х –3)2d х = ∫(х 2–6 х +9)d х = ∫ х 2d х - 6∫ х d х +9∫d х = х 3∕3 -3 х 2+9 х +С. В подавляющем большинстве случаев мы имеем дело с интегралами функций, которые нельзя найти непосредственным интегрированием. В этом случае необходимо сделать подстановку (заменить переменную).
б) Интегрирование подстановкой (замена переменной).
Интегрирование подстановкой, или как его часто называют, методом замены переменой, является одним из более эффективных и распространенных методов интегрирования. Способ подстановки состоит в том, чтобы перейти от данной переменной интегрирования к другой переменной с целью упростить подинтегральное выражение и привести его к одному из табличных видов интегралов. При этом выбор подстановки решается исполнителем индивидуально, т.к. не существует общих правил, указывающих какую подстановку в данном случае взять. Пример: Найти интеграл ∫ е 2х+3d х. Введем новую переменную t, связанную с х следующей зависимостью 2 х + 3 = t. Возьмем дифференциалы от левой и правой частей этого равенства: 2d х = dt; d х =dt/2. Теперь вместо 2 х + 3 и d х в подинтегральное выражение подставим их значения. Тогда получим: ∫ е 2х+3d х = ∫ е 2х+3d х = Чтобы убедиться в правильности взятия интеграла необходимо первообразную функцию (
3. Определенный интеграл и его свойства. Понятие определенного интеграла широко используется во многих областях науки и техники. С его помощью вычисляются площади, ограниченные кривыми, объемы произвольной формы, мощность и работа переменной силы, путь движущегося тела, моменты инерции и многие другие величины.
Поставим перед собой задачу: определить площадь S криволинейной трапеции а АоА пв. Для этого разобьем отрезок [ а,в ] на п не обязательно равных частей и обозначим точки деления таким образом: а = х о‹ х 1‹ х2 ‹ … ‹ хп = в. Из точек деления восстановим перпендикуляры до пересечения с кривой у = f(х). Таким образом, мы всю площадь, ограниченную кривой, разбили на п элементарных криволинейных трапеций. Восстановим из произвольных точек каждого отрезка ∆ хi ординаты f(С i) до пересечения с кривой у = f(х). Далее построим ступенчатую фигуру, состоящую из прямоугольников с основанием ∆ хi и высотой f(С i). Элементарная площадь i-го прямоугольника будет S i = f(С i)(хi - хi-1), а вся площадь S п полученной ступенчатой фигуры будет равна сумме площадей прямоугольников: S п Для сокращения записи этой суммы вводят символ S п = Эта сумма S п, которая называется интегральной суммой, может быть или больше или меньше истинного значения данной площади. Наиболее близким значением к истинной величине площади будет предел суммы при условии, что элементарные отрезки будут дробиться (п→ S = Этот предел интегральной суммы (если он существует) называется определенным интегралом от функции f(х) на отрезке [ а, в ] и обозначают: (читается – “определенный интеграл от а до в эф от икс дэ икс”). Числа а и в называются соответственно нижним и верхним пределами интегрирования, f(х) – подинтегральной функцией; х – переменной интегрирования. Применив формулы (4) и (5) можно записать. Что площадь криволинейной трапеции численно равна интегралу от функции, ограничивающей трапецию, взятому на интервале интегрирования [ а, в ]:
Этот факт выражает геометрический смысл определенного интеграла. Рассмотрим свойства определенного интеграла. 1. Определенный интеграл не зависит от обозначения переменной, т.е.: 2. Определенный интеграл алгебраической суммы равен алгебраической сумме определенных интегралов от каждого слагаемого:
3. Постоянный множитель к в подинтегральном выражении выносится за знак интеграла:
4. Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл изменит свой знак на противоположный, сохранив абсолютную величину неизменной:
5. Если отрезок [ а, в ] разбить на две части [ а, с ] и [ с,в ], то интеграл:
6. 7. Если подинтегральная функция на отрезке [ а, в ] сохраняет постоянный знак, то и определенный интеграл будет представлен числом того же знака, т.е.: f(х)>0 и Существуют и другие свойства определенного интеграла, которые мы рассматривать не будем.
4. Связь между определенным и неопределенным интегралами.
а) Формула Ньютона-Лейбница.
Несмотря на то, что неопределенный интеграл есть совокупность первообразных, а определенный интеграл есть число, все же между ними имеется определенная связь, впервые установленная Ньютоном и Лейбницем в виде формулы Ньютона-Лейбница. Значение определенного интеграла равно разности значений любой первообразной от подинтегральной функции, взятой при верхнем и нижнем пределах интегрирования:
Рассмотрим пример нахождения определенного интеграла. Пусть нам необходимо найти определенный интеграл вида:
Нахождение определенного интеграла сводится к следующим операциям: 1) находят первообразную для данной подинтегральной функции; 2) вычисляются первообразные для данных частных значений верхнего и нижнего пределов интегрирования; 3) находят разность частных значений первообразной F(в) – F(а). б) Применение метода замены переменной интегрирования при вычислении определенного интеграла. При использовании метода замены переменной для вычисления определенного интеграла вводится новая переменная, с помощью которой интеграл сводится к табличному. Одновременно заменяют пределы интегрирования. Рассмотрим эти операции на отдельном примере: 3) а = sin0 = 0; в = sin 4) 5. Дифференциальное уравнение. а) Общее понятие и определение. Многие вопросы естествознания, техники и различных отраслей науки сводятся к нахождению неизвестной функции, если известно уравнение, содержащее х,у и производные различных порядков функции f(х): f '(х); f "(х); f "'(х); …; f( n)(x) илидифференциалы df; d2f; d3f; …; dnf. Такие уравнения называют дифференциальными (ДУ). В общем виде ДУ можно записать так: F(х,у,у',у",…,у(п)) = 0. Для функции у = f(х) одного аргумента дифференциальные уравнения называются обыкновенными; для функции и = f(х,у,z, …,t) нескольких переменных (двух и более) уравнения называются дифференциальными в частных производных. Порядком ДУ называется порядок наивысшей производной или дифференциала. Например, у' = 2 х 2 у + 5 – уравнение 1-го порядка, а у" + у' = 0 - уравнение второго порядка. Общим решением ДУ к -го порядка называется функция у = f(х,с1,с2, …,с к) от х с произвольными постоянными с1,с2, …,с к, обращающая это уравнение в тождество. При конкретном значении произвольных постоянных получают частное решение из общего. При этом задаются не сами постоянные, а условие, которому должно удовлетворять искомое частное решение. Задание таких условий называется заданием начальных условий и кратко записывается так: при х = х о; f(х о ) = уо; f '(х о ) = у'о и т.д. Задача нахождения частного решения удовлетворяющего его начальным условиям, называется задачей Коши. б) Дифференциальные уравнения первого порядка с разделяющимися переменными. Дифференциальные уравнения вида: f1(x)φ1(y)d x + f2(x)φ2(y)dy = 0 называются дифференциальными уравнениями с разделяющимися переменными. Суть такого разделения сводится к тому, чтобы путем некоторых математических операций, произвести группировку переменных, производных, дифференциалов в отдельные слагаемые так, чтобы, они содержали только один вид переменных. Слагаемые, включающие только одну переменную, можно получить, если ДУ разделить на f2(x)φ2(y). Тогда получим: Интегрируя это уравнение, мы получим общее решение дифференциального уравнения в виде: Пример: 1) у' = 2 х у; ln y = ln ex 2) у' = 4 х3 (при х =0, у =0). ∫dy = 4∫ x3dx;y = x 4 + c; y = x 4.
6. Линейные однородные уравнения второго порядка с постоянными коэффициентами.
Уравнение вида: y"+py'+qy=f(x), где p, q – постоянные коэффициенты, а f(x) – некоторая функция, называют линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами. Мы рассмотрим уравнение для случаев когда f(x)=0. Если f(x)=0, то уравнение y"+py'+qy=0 называют линейным однородным дифференциальным уравнением (ЛОДУ) второго порядка с постоянными коэффициентами. Решение такого дифференциального уравнения, как показал Эйлер, следует искать в виде следующих функций: у = е кх, где к – некоторый коэффициент. Подставим значения у' = кек х и у" = к 2е кх, найденные из этой функции в уравнение. Тогда получим: к 2е кх + к pе кх + qe кх = 0 или е кх (к2 + p к +q) = 0; е кх ≠ 0. Для того чтобы функция у=е кх была решением дифференциального уравнения, достаточно, чтобы к2 + p к +q = 0. Это уравнение называют характеристическим уравнением и корни его определяются по формуле: к1,2 = - Эйлер показал, что для ЛОДУ может быть три вида решений: 1-ый вид: если корни к 1 и к 2 характеристического уравнения действительные и различные (к 1 ≠ к 2), то все решения ЛОДУ даются формулой: у = с1 ∙ 2-ой вид: если корни к 1 и к 2 характеристического уравнения действительные и равные к 1 = к 2 = к, то все решения ЛОДУ даются в виде такой формулы: у = (с1 + с2) е кх. 3-й вид: если же корни к1,2 = Все приведенные выше три вида решений представляют собой общеерешение ЛОДУ. Частные решения находят по заданным начальным условиям: Пример: у"–6у'+8у = 0; к2 -6 к +8 = 0; к1,2 = 3 у = с1 ∙ е4 х + с2 ∙ е2 х . ЛЕКЦИЯ №3
|

 ∫ е tdt =
∫ е tdt =  В подавляющем большинстве случаев понятие определенного интеграла вводится при решении задач определения площади криволинейной трапеции. Пусть имеется непрерывная функция у = f(х) на отрезке [ а,в ]. Фигуру, ограниченную кривой у= f(х) ординатами а Ао, в А п и отрезком [ а,в ] оси абсцисс называют криволинейной трапецией (рис.1).
В подавляющем большинстве случаев понятие определенного интеграла вводится при решении задач определения площади криволинейной трапеции. Пусть имеется непрерывная функция у = f(х) на отрезке [ а,в ]. Фигуру, ограниченную кривой у= f(х) ординатами а Ао, в А п и отрезком [ а,в ] оси абсцисс называют криволинейной трапецией (рис.1). = f(Со)(х 1 –х о) + f(С1)(х2 –х1 ) + … + f(С п- 1)(х п –хп- 1).
= f(Со)(х 1 –х о) + f(С1)(х2 –х1 ) + … + f(С п- 1)(х п –хп- 1). (сигма) – знак, означающий суммирование величин. Тогда
(сигма) – знак, означающий суммирование величин. Тогда .
. ), а длина самого большого отрезка ∆ хmax будет стремиться к нулю, т.е.:
), а длина самого большого отрезка ∆ хmax будет стремиться к нулю, т.е.: (4)
(4) =
=  .
. =
=  .
. [f1(х) + f2(х) + … d х ] =
[f1(х) + f2(х) + … d х ] =  f(х) d х.
f(х) d х. f(х) d х +
f(х) d х +  f(х) d х.
f(х) d х. = F(в) -F(а).
= F(в) -F(а). =
=  .
. ; 1) sin x = t; 2) d(sin x) = dt; cos x d x = dt;
; 1) sin x = t; 2) d(sin x) = dt; cos x d x = dt; ;
;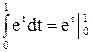 = е1 – е0 =2,7 –1 =1,7.
= е1 – е0 =2,7 –1 =1,7. .
. . Это выражение является общим решением приведенного уравнения.
. Это выражение является общим решением приведенного уравнения. = 2 х у;
= 2 х у;  = 2 х d x;
= 2 х d x;  ; ln y = x 2 + C;
; ln y = x 2 + C; + ln C;
+ ln C;  ; у = с · e x
; у = с · e x  - общее решение. При начальных условиях х =0, у = 2; с =2; у = 2 e x
- общее решение. При начальных условиях х =0, у = 2; с =2; у = 2 e x  - частное решение.
- частное решение.
 + с2 ∙
+ с2 ∙  .
. ; (i =
; (i =  ) характеристического уравнения комплексные числа, то все решения ЛОДУ даются такой формулой: у = еα x (с1cos β x +c2sin β x), где с1 и с2 - произвольные постоянные.
) характеристического уравнения комплексные числа, то все решения ЛОДУ даются такой формулой: у = еα x (с1cos β x +c2sin β x), где с1 и с2 - произвольные постоянные. ; к 1 =4; к2 = 2;
; к 1 =4; к2 = 2;


