ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
1. Случайное событие. Вероятность случайного события.
В теории вероятностей исследуются закономерности, относящиеся к случайным событиям, величинам, процессам. Теория вероятностей служит для обоснования математической и прикладной статистики. В естественных науках понятие «статистика» означает анализ массовых явлений, основанный на применении методов теории вероятности. Математическая статистика – это наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятности, позволяющую оценить надежность и точность выводов на основе ограниченного статистического материала. Среди множества методов познания биологических процессов теория вероятности с математической статистикой занимает одно из важных мест. Массовые явления и процессы характеризуются, прежде всего, многократным повторением при постоянных условиях некоторых опытов, операций и т.д. Всякий факт какого-либо испытания, эксперимента или действия называют событием. Событие – это исход испытания. События называются достоверными, если они происходят неизбежно в результате каждого испытания и невозможными, если в результате каждого испытания они не могут произойти. Одним из важных понятий теории вероятности является понятие «случайного события». Случайным событием называется всякий факт, который в результате опыта (испытания) может произойти или не произойти. Например, случайными будут события: успешная сдача студентом экзамена, вспышка эпидемии, появление герба при бросании монеты, попадание в цель при выстреле. Рассматривая множество событий, можно предположить, что для каждого случайного события объективно существует специфическая мера возможности его появления в данном опыте, называемая вероятностью события. Эта безразмерная величина, служащая в некотором смысле «мерой случайности» события, характеризующая степень его близости к достоверному событию. Вероятность любого события А обозначается символом Р(А) или РА или Р. Классической вероятность Р(А) события А называется отношение числа случаев m, благоприятствующих событию А, к общему числу случаев n (n –мало): Р(А) = Вероятность любого события А удовлетворяет двойному неравенству: 0 ≤ Р(А) ≤1, так как вероятность достоверного события равна 1; невозможного – 0. Если же имеется возможность неограниченного повторения испытания, то при достаточно большом n испытаний интересующее нас событие А может произойти m раз, а отношение Р* (А) = В ряде случаев вычислить вероятность события оказывается проще, если представить его в виде комбинации более простых событий. Этой цели служат теоремы сложения и умножения вероятностей. Пусть события А и В несовместны и известны их вероятности. Вероятность осуществления либо события А, либо события В определяется теоремой сложения. Вероятность появления одного из двух несовместных событий равна сумме их вероятностей: Р(А или В) = Р(А) + Р(В). Доказательство: Пусть n – общее число испытаний; m1 – число случаев, благоприятствующих событию А; m2 – число случаев, благоприятствующих событию В. Число случаев, благоприятствующих наступлению события А, либо события В, равно m1 + m2. Тогда Р(А или В) = Пример: Найти вероятность выпадания “1” или “6” при бросании игральной кости. Событие А (выпадание 1) и В (выпадание 6) является равновозможными: Р(А) = Р(В) = Теорема умножения вероятностей заключается в следующем. Вероятность совместного появления независимых событий равна произведению их вероятностей. Для двух событий: Р(А и В) = Р(А) · Р(В). Доказательство: Пустьm1 - число случаев, благоприятствующих событию А; m2 - число случаев, благоприятствующих событию В; n1 – число равновозможных случаев, в которых событие А появляется или нет. n2 - число равновозможных случаев, в которых событие В появляется или нет. Общее число случаев, благоприятствующих совместному появлению событий А и В равно m1 m2. Общее число возможных элементарных событий испытания равно n1 n2 (число событий n1 может сочетаться с каждым из n2 событий). Вероятность совместного появления событий А и В – Р(А и В)= Пример: В одной урне находится 5 черных и 15 белых шаров, в другой – 3 черных и 17 белых шаров. Найти вероятность того, что при первом вынимании шаров из каждой урны оба шара окажутся черными: Р(А и В) = Р(А) · Р(В) =
2. Случайные величины. Закон распределения и числовые характеристики дискретных случайных величин.
Каждому элементарному событию Х из некоторого множества событий можно поставить в соответствие то или иное значение х, которое будет являться случайной величиной. Примером случайной величины могут являться: количество студентов на лекции, продолжительность жизни человека, ошибка при измерении той или иной величины, количество больных на приеме у врача. Случайные величины служат основным объектом теории вероятности и математической статистики. Различают два основных типа случайных величин: дискретные и непрерывные. Дискретной (прерывной) называют случайную величину, принимающую на заданном интервале конечное или бесконечное множество отдельных значений, элементы которого могут быть занумерованы в каком-либо порядке и записаны в последовательности: х1, х2, …, хп. Примером дискретной случайной величины, принимающей бесчисленное множество значений на конечном интервале, может быть множество всех рациональных чисел на интервале ]0,1[, число букв на произвольной странице текста., число родившихся мальчиков в различные месяцы в определенном регионе. Дискретная случайная величина считается заданной, если указаны все ее возможные значения и соответствующие им вероятности. Обозначим дискретную случайную величину X, а ее значение х1, х2, х3,,…, соответствующие им вероятности Р(х 1) = Р1; Р(х 2) = Р2 и т.д.. Законом распределения дискретной случайной величины называют всякое соответствие, устанавливающее связь между ее возможными значениями и их вероятностями. Закон распределения может иметь различные формы. Он может быть задан в виде таблицы, которую также называют рядом распределения:
Так как все возможные случайные величины образуют полную группу событий (представляют полную систему), то сумма их вероятностей равна единице: Закон распределения полностью описывает дискретную случайную величину. Во многих случаях наряду с законом или вместо него информацию о случайных величинах могут дать числовые параметры, получившие название числовых характеристик дискретных случайных величин. Рассмотрим наиболее употребляемые из них: 1. Математическое ожидание дискретной случайной величины х – это сумма произведений всех возможных значений величины х на вероятности этих значений: Оно соответствует значению случайной величины, около которого группируются все его возможные значения. При большом числе измерений среднее арифметическое случайной величины приближается к ее математическому ожиданию. Если произведено n независимых испытаний, в которых случайная величина принимает значение х 1 – m1 раз, х 2 – m2 раз … х n – mn раз, то: m1+ m2+…+ mn = n. Среднее арифметическое всех значений случайной величины:
Следовательно, равенство тем точнее, чем больше число наблюдений n и при большом числе n испытаний 2. Дисперсией дискретной случайной величины х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Слово «дисперсия» означает «рассеяние». Дисперсия обозначается D(X) или
3. Средним квадратичным отклонением называется корень квадратный из дисперсии: Эта величина вводится для оценки рассеяния случайной величины вокруг ее математического ожидания. Она имеет размерность, совпадающую с размерностью случайной величины X.
3. Непрерывные случайные величины. Нормальный закон распределения (закон Гаусса).
Для описания реальных величин, зависящих от случая, дискретных случайных величин недостаточно. Действительно, таким величинам как температура, давление, размеры физических объектов, длительность физических процессов неестественно приписывать дискретное множество возможных значений. Естественно считать, что их возможные значения в принципе могут быть любыми числами в некоторых пределах, т.е. являться непрерывными случайными величинами. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного интервала. Число возможных значений непрерывной случайной величины бесконечно. Непрерывную случайную величину нельзя описать законом распределения как дискретную в виде таблицы. Однако различные области возможных ее значений все же не являются одинаково вероятными, и для непрерывной случайной величины существует «распределение вероятностей», хотя не в том смысле, что для дискретной. Для конечной оценки распределения вероятностей удобно пользоваться не вероятностью события Х=х, а вероятностью события Х ‹ х. Под выражением Х ‹ х понимают событие – «случайная величина Х приняла значение, меньшее х». Функцией распределения случайной величины X называется функция F(х), равная вероятности Р(Х ‹ х) того, что случайная величина X принимает значение, меньшее х: F(х) = Р(Х ‹ х). Функцию F(х) называют еще «интегральной функцией распределения» или интегральным законом распределения. Функция F(х) является одной из форм закона распределения. Однако в большинстве случаев для описания непрерывных случайных величин при теоретическом их изучении вводят понятие плотности распределения (плотность вероятности), которая равна производной ее интегральной функции f(x) = F'(х). Наиболее часто встречаются величины, распределенные по нормальному закону распределения (закону Гаусса), являющемуся предельным законом, к которому приближаются другие законы распределения. Случайная величина распределяется по нормальному закону, если плотность вероятности ее имеет вид: f(x) = где μ – математическое ожидание,
Площадь, ограниченная кривой нормального распределения всегда равна единице, поэтому при увеличении σ кривая становится пологой.
4. Статистическое распределение выборки. Гистограмма.
На практике всегда приходится иметь дело с ограниченным количеством экспериментальных данных, поэтому результаты наблюдений и их обработка содержит больший или меньший элемент случайности. Разработка методов регистрации, описания и анализа таких экспериментальных данных составляет предмет математической статистики. В математической статистике изучение случайной величины связано с выполнением ряда независимых опытов, в которых она принимает определенное значение. Полученные значения случайной величины представляют простой статистический ряд (простая статистическая совокупность), подлежащий обработке и научному анализу. Общее число членов этого ряда называют его объёмом. Совокупность, состоящая из всех объектов, которые могут быть к ней отнесены, называется генеральной (количество больных на земном шаре, страдающих гипертонией). Теоретически это бесконечно большая или приближающаяся к бесконечности совокупность. Число объектов генеральной совокупности называется ее объемом N. Множество объектов, случайно отобранных из генеральной совокупности, называется выборочной совокупностью или выборкой, а число объектов выборки называется ее объемом и обозначается буквой (п). Первой задачей статистической обработкти экспериментального материала является наведение опреленного порядка в полученном простом статистическом ряду. Поэтому целесообразно расположить данные в порядке возрастания с указанием их повторяемости – составить вариационный ряд. Если количественный признак является дискретным, подсчитывают сколько раз встречается каждое значение признака и результат представляют в виде таблицы:
Наблюдаемые значения х 1, х 2, …, хп называют вариантами. Числа m1, m2, …, m n - называют частотами, а их отношение к объёму выборки относительными частотами: Р*i = Сумма всех частот равна объему совокупности п: Таблицу, содержащую значение вариант признака, их частоты или относительные частоты, называют дискретным статистическим рядом распределения или статистическим распределением выборки. В случае большего количества вариант и непрерывности признака дискретный ряд перестает быть удобной формой записи статистического материала. В этом случае производят группировку вариант по интервалам, при этом весь диапазон признака х делят на определенное число k интервалов шириной ∆ х, подсчитывают частоту m i в каждом интервале, значения, попавшие на конец интервала, относят или к левому или к правому интервалу, определяют Рi* =
Число интервалов определяется по формуле Стерджесса k = 1 + 3,332 lg n, где n – объем выборки, а ширина интервала: ∆ х =
Полученную таким образом ступенчатую фигуру, состоящую из прямоугольников, называют гистограммой. Площадь всех прямоугольников будет равна единице. При неограниченном увеличении числа наблюдений п и уменьшении ширины интервалов верхняя ломанная линия будет стремиться к плавной кривой, ограничивающей площадь, равную единице. В пределе плавная кривая будет графиком плотности вероятности, которая и характеризует плотность распределения случайной величины. При большом числе наблюдений на гистограмме появляются основные статистические закономерности: 1. Полученные в наблюдениях значения измеряемой величины симметрично расположены около некоторого среднего значения х. 2. Большие отклонения от среднего х встречаются реже, чем малые. 5. Обработка результатов прямых и косвенных измерений. а) Погрешности измерений. Количественная сторона процессов и явлений в любом эксперименте изучается с помощью измерений, которые делятся на прямые и косвенные. Прямым называется такое измерение, при котором значение, интересующее экспериментатора величины находятся непосредственно из отсчета по прибору. Косвенное - это измерение, при котором значение величины находится как функция других величин. Например, сопротивление резистора определяют по напряжению и току (R = Измеренное значение х изм. некоторой физической величины х обычно отличается от ее истинного значения х ист.. Отклонение результата, полученного на опыте, от истинного значения, т.е. разность х изм.– х ист. = ∆ х – называется абсолютной ошибкой измерения, а Систематическими ошибками называются такие ошибки, величина и знак которых от опыта к опыту сохраняется или изменяется закономерно. Они искажают результат измерений в одну сторону – либо завышая, либо занижая его. Подобные ошибки вызываются постоянно действующими причинами, односторонне влияющие на результат измерений (неисправность или малая точность прибора). Ошибки, величина и знак которых непредсказуемым образом изменяются от опыта к опыту, называются случайными. Такие ошибки возникают, например, при взвешивании из-за колебаний установки, неодинакового влияния трения, температуры, влажности и т.д. Случайные ошибки возникают и из-за несовершенства или дефекта органов чувств экспериментатора. Случайные погрешности исключить опытным путем нельзя. Их влияние на результат измерения может быть оценено с помощью математических методов статистики (малые выборки). Промахами или грубыми погрешностями называются погрешности, существенно превышающие систематические и случайные погрешности. Наблюдения, содержащие промахи отбрасываются как недостоверные. б) Обработка результатов непосредственных измерений. Для надежности оценки случайных погрешностей необходимо выполнить достаточно большое количество измерений п. Допустим, что в результате непосредственных измерений получены результаты х 1, х 2, х 3, …, хп. Наиболее вероятное значение определяется как среднее арифметическое, которое при большом числе измерений совпадает с истинным значением: Затем определяют среднюю квадратичную ошибку отдельного измерения: При этом можно оценить наибольшую среднюю квадратичную ошибку отдельного измерения: Sнаиб. = 3S. Следующий этап заключается в определении средней квадратичной ошибки среднего арифметического:
Ширина доверительного интервала около среднего значения Эту запись можно понимать как неравенство: Относительная погрешность: в) Обработка результатов косвенных измерений. Если величину у измеряют косвенным методом, т.е. она является функцией п независимых величин х 1, х 2, …, хп: у = f(х 1, х 2, …, хп), а значит
где частные производные вычисляются для средних значений 6. Понятие о корреляционном анализе.
Функциональная зависимость величин достаточно хорошо знакома, и часто эту зависимость можно выразить аналитически: S =πr2; S =f (r); a= Однако существует зависимость между величинами, связанными не только функционально, но и статистически. При научных исследованиях изучаются зависимости, которые не слишком очевидны и не выражаются простыми однозначными формулами. Так, например, зависимость между дозой лекарственного препарата (х) и содержанием его в крови (у), которое определяется не только количеством препарата, но и массой больного, скорость выведения препарата из организма, наличием в крови других веществ и т.д. Прослеживается связь между ростом людей и массой их тела, между погодными условиями и количеством простудных заболеваний населения. Такая, более сложная, чем функциональная, вероятностная зависимость является корреляционной зависимостью(или просто корреляция). Корреляционная зависимость – это частный случай статистической зависимости между величинами, когда изменение одной из величин, например, Х влечет к изменению среднего значения (или математического ожидания) другой –У. При изучении связи между Х и У каждому значению Х= х будет соответствовать несколько значений У: у1, у2, у3 и т.д. Условным средним Уравнение (1) называется уравнением регрессии у на х, а график функции – линией регрессии у на х. Аналогично можно сформулировать корреляционную зависимость Х от У: Достоверность корреляционной зависимости может быть оценена коэффициентами линейной корреляции. Более подробно этот материал рассматривается в курсе социальной гигиены и организации здравоохранения. ЛЕКЦИЯ №4
|

 .
. - называется относительной частотой события А или просто частотой события А. Частоту события иначе называют статистической вероятностью. При большом числе испытаний частота события примерно постоянная величина.
- называется относительной частотой события А или просто частотой события А. Частоту события иначе называют статистической вероятностью. При большом числе испытаний частота события примерно постоянная величина. = Р(А) + Р(В).
= Р(А) + Р(В). ; Р(А или В) =
; Р(А или В) =  .
. = Р(А) · Р(В).
= Р(А) · Р(В). .
. .
.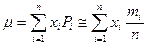 .
. ;
; стремится к Рi.
стремится к Рi. или
или  . По определению:
. По определению: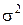 =
=  (хi – μ)2 Pi.
(хi – μ)2 Pi.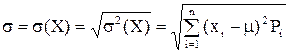 .
.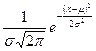 ,
,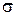 - среднее квадратическое отклонение.
- среднее квадратическое отклонение. График плотности вероятности нормального распределения носит название нормальной кривой распределения или кривой Гаусса (рис.1). В точке х = μ функция имеет максимум: f(μ) =
График плотности вероятности нормального распределения носит название нормальной кривой распределения или кривой Гаусса (рис.1). В точке х = μ функция имеет максимум: f(μ) =  . Форма кривой распределния зависит от σ (рис.2); μ – определяет центр рассеяния, а значит и положение распределения на оси абцисс (рис.3). При этом кривая сохраняет свою форму.
. Форма кривой распределния зависит от σ (рис.2); μ – определяет центр рассеяния, а значит и положение распределения на оси абцисс (рис.3). При этом кривая сохраняет свою форму.
 .
. .
. Имея указанную таблицу, на оси 0 х откладывают интервал длиной ∆ х, а по оси 0у откладывают плотность относительной частоты
Имея указанную таблицу, на оси 0 х откладывают интервал длиной ∆ х, а по оси 0у откладывают плотность относительной частоты  . На каждом частотном интервале строят прямоугольник с основанием ∆ х и высотой
. На каждом частотном интервале строят прямоугольник с основанием ∆ х и высотой 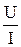 ).
). – относительной ошибкой (погрешностью) измерения. Погрешности или ошибки делятся на систематические, случайные и промахи.
– относительной ошибкой (погрешностью) измерения. Погрешности или ошибки делятся на систематические, случайные и промахи. .
. .
. .
.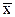 измеряемой величины будет определяться поабсолютной погрешности среднего арифметического:
измеряемой величины будет определяться поабсолютной погрешности среднего арифметического:  , где tα,n – так называемый коэффициент Стьюдента для числа наблюдений п и доверительной вероятности α (табличная величина). Обычно доверительная вероятность в условиях учебной лаборатории выбирается 0,95 или 95%. Это значит, что при многократном повторении опыта в одних и тех же условиях, ошибки, в 95 случаях из 100 не превысят значения
, где tα,n – так называемый коэффициент Стьюдента для числа наблюдений п и доверительной вероятности α (табличная величина). Обычно доверительная вероятность в условиях учебной лаборатории выбирается 0,95 или 95%. Это значит, что при многократном повторении опыта в одних и тех же условиях, ошибки, в 95 случаях из 100 не превысят значения  . Интервальной оценкой измеряемой величины x будет доверительный интервал
. Интервальной оценкой измеряемой величины x будет доверительный интервал  , в который попадает её истинное значение с заданной вероятностью α. Результат измерения записывается:
, в который попадает её истинное значение с заданной вероятностью α. Результат измерения записывается: 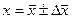 .
. .
.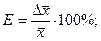 Е ≤ 5% в условиях учебной лаборатории.
Е ≤ 5% в условиях учебной лаборатории. . Средняя квадратичная ошибка среднего арифметического определяется по формуле:
. Средняя квадратичная ошибка среднего арифметического определяется по формуле: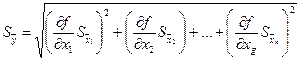 ,
, вычисляется по формуле средней квадратичной ошибки для непосредственного измерения. Доверительная вероятность для всех погрешностей, связанных с аргументами хi функции у задается одинаковый (Р = 0,95), такой же она задается и для у. Абсолютная погрешность
вычисляется по формуле средней квадратичной ошибки для непосредственного измерения. Доверительная вероятность для всех погрешностей, связанных с аргументами хi функции у задается одинаковый (Р = 0,95), такой же она задается и для у. Абсолютная погрешность  среднего значения
среднего значения  определяется по формуле:
определяется по формуле:  . Тогда
. Тогда 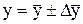 или
или  . Относительная погрешность
. Относительная погрешность  будет равна Е =
будет равна Е =  ≤5%.
≤5%.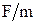 ; a = f (F,m).
; a = f (F,m).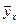 назовем среднее арифметическое значение у (или математическое ожидание у), соответствующее значению Х= х. Тогда корреляционную зависимость или корреляцию У от Х можно записать:
назовем среднее арифметическое значение у (или математическое ожидание у), соответствующее значению Х= х. Тогда корреляционную зависимость или корреляцию У от Х можно записать: 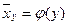 (2) или М(X)y.=φ(y). Если обе функции (1) и (2) являются линейными, то корреляция называется линейной, в противном случае нелинейной.
(2) или М(X)y.=φ(y). Если обе функции (1) и (2) являются линейными, то корреляция называется линейной, в противном случае нелинейной.


