ЧЕЛОВЕКА.
1. Основные законы кинематики вращательного движения.
При этом положение тела в любой момент времени определяется углом поворота φ радиуса вектора R любой точки А относительно своего начального положения. Зависимость его от времени:
является уравнением вращательного движения. Быстрота вращения тела характеризуется угловой скоростью ω. Угловая скорость всех точек вращательного тела одинакова. Она является векторной величиной. Этот вектор направлен по оси вращения и связан с направлением вращения правилом правого винта:
При равномерном движении точки по окружности
где Δφ=2π – угол, соответствующий одному полному обороту тела, Δt=T – время одного полного оборота, или период вращения. Единица измерения угловой скорости [ω]=c-1. При равномерном движении ускорение тела характеризуется угловым ускорением ε (вектор его расположен аналогично вектору угловой скорости и направлен согласно с ним при ускоренном и в обратном направлении – при замедленном движении):
Единица измерения углового ускорения [ε]=c-2. Вращательное движение можно характеризовать также линейной скоростью и ускорением его отдельных точек. Длина дуги dS, описываемой любой точкой А (рис.1) при повороте на угол dφ определяется по формуле: dS=Rdφ. (5) Тогда линейная скорость точки
Линейное ускорение а:
2. Основные законы динамики вращательного движения. Вращение тела вокруг оси вызывается силой F, приложенной к любой точке тела, действующей в плоскости перпендикулярной оси вращения и направленной (или имеющей составляющую в этом направлении) перпендикулярно радиусу вектору точки приложения (рис.1). Моментом силы
Момент
Мерой инертности тела при поступательном движении является масса. При вращении тела мера его инертности характеризуется моментом инерции тела относительно оси вращения. Моментом инерции Ii материальной точки относительно оси вращения называют величину, равную произведению массы точки на квадрат расстояния её от оси (рис.2):
Моментом инерции тела относительно оси называют сумму моментов инерции материальных точек, из которых состоит тело:
Или в пределе (n→∞):
Момент инерции человека относительно вертикальной оси вращения, проходящей через центр масс (центр масс человека находится в сагиттальной плоскости несколько впереди второго крестового позвонка), в зависимости от положения человека имеет следующие значения: 1,2 кг·м2 при стойке «смирно»; 17 кг·м2 – в горизонтальном положении. При вращении тела его кинетическая энергия складывается из кинетических энергий отдельных точек тела:
Продифференцировав (14), получим элементарное изменение кинетической энергии:
Приравняв элементарную работу (формула 9) внешних сил к элементарному изменению кинетической энергии (формула 15), получим: Это уравнение называется основным уравнением динамики вращательного движения. Эта зависимость аналогична II закону Ньютона для поступательного движения. Моментом импульса Li материальной точки относительно оси называется величина, равная произведению импульса точки на расстояние её до оси вращения:
Момент импульса L тела, вращающегося вокруг неподвижной оси:
Момент импульса есть векторная величина, ориентированная по направлению вектора угловой скорости. Теперь возвратимся к основному уравнению (16):
Подведём постоянную величину I под знак дифференциала и получим: где Mdt называют импульсом момента силы. Если на тело не действуют внешние силы (М=0), то равно нулю и изменение момента количества движения (dL=0). Это означает, что момент импульса остаётся постоянным: Этот вывод называется законом сохранения момента импульса относительно оси вращения. Его используют, например, при вращательных движениях относительно свободной оси в спорте, например в акробатике и т.д. Так, фигурист на льду, изменяя в процессе вращения положение тела и соответственно момент инерции относительно оси вращения, может регулировать свою скорость вращения.
3. Механические свойства тканей. Механические свойства тканей необходимо учитывать гигиенистам при защите человека от вибраций, в протезировании при замене естественных органов и тканей искусственными, в судебной медицине. В травматологии и ортопедии необходимо знать устойчивость биологических структур по отношению к различным деформациям, в спорте и космонавтике обращают внимание на физические возможности опорно-двигательного аппарата и т.д.
где F – внешняя сила; S – площадь поперечного сечения;
Для этого элемента существует зависимость:
Вязкоупругие свойства различных тканей можно отразить системами механических моделей, состоящих из различных комбинаций двух простых моделей (рис.5). Обращают на себя внимание две особенности поведения таких сложных систем. Во-первых, под действием постоянной силы длина изменяется не мгновенно, а во времени. Это явление называется ползучестью. Наиболее простой системой, сочетающей упругие и вязкие свойства, является тело Максвелла (рис.5б). При воздействии постоянной силой пружина упруго мгновенно удлиняется до значения определяемого законом Гука (до Δlу), а поршень движется с постоянной скоростью до тех пор, пока действует сила. Так реализуется на модели ползучесть материала
(рис.6).
При приложении растягивающей силы к гладким мышцам они ведут себя в основном подобно телу Максвелла. Поэтому гладкие мышцы могут значительно растягиваться без особого напряжения. Это способствует большой растяжимости полых органов, содержащих гладкие мышцы, например, мочевого пузыря. Скелетная мышца в покое по механическому поведению представляет третью модель (рис.5в). при внезапном растяжении этой мышцы на определённую величину напряжение резко возрастает, а затем уменьшается до определённого равновесного уровня. Но в отличие от этой механической модели мышца характеризуется нелинейной зависимостью напряжения от длины. И модуль упругости этой мышцы, в отличие от модели, не будет постоянным, а будет различным при различных нагрузках. Кости в соответствии с их опорной и защитной функциями резко отличаются по механическим свойствам от мышц и других биоматериалов. Минеральное содержание кости обеспечивает быструю деформацию, а полимерная часть определяет ползучесть. При небольших деформациях для костей справедлив закон Гука. Модуль упругости кости может достигать около ЕК=109 Н/м2, что на несколько порядков выше модуля упругости мышц. Кости характеризуются очень большой механической прочностью. Её механическое разрушение начинается при σ=107-108 Н/м2 (для тканей стенок крупных артерий разрушение начинается при σ=106 Н/м2). Стенки кровеносных сосудов построены из вязкоэластичного материала (за исключением капилляров). Поэтому крупные сосуды способны к значительным обратимым изменениям размера при действии на их стенку внешней силы. Упругие свойства и прочность тканей, за исключением костной, в основном определяются эластиновыми и коллагеновыми волокнами и их комплексами. На долю этих волокон, например, в стенках крупных сосудов, приходится около 50% сухой массы. Обладая высоким модулем упругости (эластиновые нити ЕЭЛ=106 Н/м2, коллагеновые нити ЕКЛ=107Н/м2) и прочностью, эти волокна предотвращают разрыв сухожилий, стенок кровеносных сосудов и др. тканей. Прочность костей обусловлена наличием «стекловолокнистых» структур, построенных из коллагена и кристаллов гидроксилапатита. 4. Биомеханические процессы в опорно-двигательном аппарате человека. Опорно-двигательный аппарат человека состоит из сочленённых между собой костей скелета, к которым в определённых точках прикрепляются мышцы. Кости соединяются между собой в суставах.
Основной механической характеристикой сустава является число степеней свободы в нём, равное числу осей, вокруг которых возможно вращение сочленённых костей. Напомним, что числом степеней свободы любой механической системы называют число независимых координат, необходимых для описания всех возможных движений системы. Рассмотрим систему из 2-х звеньев А и В, соединённых осью (рис.8). Это одноосное двухзвеньевое соединение. При неподвижном звене А звено В имеет одну степень свободы. Примером такого соединения в организме человека являются плечелоктевое, надпяточное и фаланговые соединения. Они допускают только возможность сгибания и разгибания с одной степенью свободы. Пример трёх звеньевого соединения элементов А, В и С с осями 00 и 0׀0׀ дан на рис.9. При одном направлении осей система называется одноосной. Двухосное соединение допускает вращение звеньев по двум взаимно перпендикулярным осям. При неподвижном звене А звено В обладает одной степенью свободы, в том числе и ось 0׀0׀. Звено С, вращаясь вокруг оси 0׀0׀, имеет ещё одну степень свободы, т.е. две. Примером такого соединения является лучезапястный сустав, в котором осуществляется сгибание и разгибание, а также приведение и отведение кисти.
Вторым примером (рис.11б) является действие свода стопы при подъёме на полупальцы. Преодолеваемая сила R – сила тяжести тела, приложенная к таранной кости, действующая мышечная сила F, осуществляющая подъём тела, передаётся через ахиллово сухожилие и приложена к выступу пяточной кости. Ось вращения проходит через головки плюсневых костей.
Если рассматривать скелет как совокупность отдельных звеньев, соединённых в один механизм, то окажется, что все эти звенья при нормальной стойке образуют систему, находящуюся в крайне неустойчивом равновесии. И если вся система находится в равновесии, то только благодаря постоянному напряжению поддерживающих систему мышц. Активную часть опорно-двигательного аппарата составляют мышцы. Под действием нервных импульсов они сокращают свою длину, развивая при этом определённые усилия. Такое сокращение мышцы называется изотоническим. Имеется и другой вид сокращения, при котором мышца развивает усилие, не изменяя свою длину. Оно называется изометрическим. Такое сокращение даёт возможность удерживать предметы и орудия труда. При сокращении мышцы будут выполняться механическая работа Р·х (х – величина укорочения мышцы; Р – вес нагрузки) и выделяется теплота qХ (теплопродукция), которая равна работе А, затрачиваемой на укорочение самой мышцы. Общая работа сокращения Возможной характеристикой мышечного сокращения является скорость сокращения - Ещё в 1938 г. Хилл показал, что в случае работы мышц между Р, В первой серии опытов он определял выделяемое мышцей тепло в ходе её сокращения в изотоническом режиме, когда Р постоянная величина. Измерения qХ проводилось при различных Р и x.
При изометрическом сокращении мышца находится в сокращённом состоянии и потребляет энергию, которая переходит в теплоту, выделяющуюся в самой мышце. Теория Хилла позволила раскрыть в некоторой мере механизм работы мышцы как идеального механизма, созданного природой. Здесь обнаруживается единство как механической, так и тепловой энергий. Исследование работоспособности мышц, измерения механической работы, совершаемой человеком в различных условиях, а также влияние этой работы на организм называется эргометрией, а соответствующие приборы – эргометрами. Когда нет перемещения, работа равна нулю. Однако, каждому знакома усталость мышцы руки или плеча, если держать неподвижно на вытянутой руке гирю или другой предмет. Груз здесь неподвижен и работы нет, но усталость свидетельствует о том, что мышцы совершают работу. Такую работу называют статической работой мышц. На самом деле и здесь происходят незаметные для глаза и очень частые мелкие сокращения и расслабления, и при этом совершается работа против сил тяжести. Таким образом, статическая работа мышц человека на самом деле является обычной динамической работой.
Работу за один оборот колеса 1 велоэргометра можно найти по формуле
Отсюда мощность, развиваемая человеком и создающая нагрузку на его сердце, будет:
ЛЕКЦИЯ №5
|

 Вращательные движения тела вокруг неподвижной оси является наиболее простым видом движения. Оно характеризуется тем, что любые точки тела описывают окружности, центры которых расположены на одной прямой 0ﺍ 0ﺍﺍ, которая называется осью вращения (рис.1).
Вращательные движения тела вокруг неподвижной оси является наиболее простым видом движения. Оно характеризуется тем, что любые точки тела описывают окружности, центры которых расположены на одной прямой 0ﺍ 0ﺍﺍ, которая называется осью вращения (рис.1). (1)
(1) . (2)
. (2)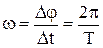 , (3)
, (3) . (4)
. (4) :
: . (6)
. (6) . (7)
. (7) относительно центра вращения называют векторную величину, численно равную произведению силы
относительно центра вращения называют векторную величину, численно равную произведению силы  на длину перпендикуляра d, опущенного из центра вращения на направление силы, называемого плечом силы. На рис.1 d=R, поэтому
на длину перпендикуляра d, опущенного из центра вращения на направление силы, называемого плечом силы. На рис.1 d=R, поэтому . (8)
. (8) . (9)
. (9) . (10)
. (10) . (11)
. (11) , (12)
, (12)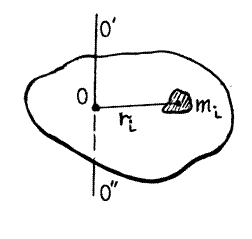 где интегрирование производится по всему объёму V. Подобным образом вычисляются моменты инерции однородных тел правильной геометрической формы. Момент инерции выражается в кг·м2.
где интегрирование производится по всему объёму V. Подобным образом вычисляются моменты инерции однородных тел правильной геометрической формы. Момент инерции выражается в кг·м2.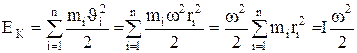 . (14)
. (14) . (15)
. (15) , откуда:
, откуда:  или, учитывая, что
или, учитывая, что  получим:
получим:  . (16)
. (16) . (17)
. (17) . (18)
. (18) ,
, 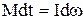 .
. , (19)
, (19) . (20)
. (20) Биологические структуры, такие как мышцы, сухожилия, кровеносные сосуды, легочная ткань и др. представляют собой вязкоупругие или упруговязкие системы. Их свойства проявляются при действии внешней силы и можно продемонстрировать сочетанием упругих и вязких элементов. Упругие и вязкие свойства тел удобно моделировать. Это даёт возможность наглядно представить механические свойства биологических объектов. Примером модели упругого элемента является идеально упругая пружина (рис.3), в которой процесс деформации происходит мгновенно и подчиняется закону Гука:
Биологические структуры, такие как мышцы, сухожилия, кровеносные сосуды, легочная ткань и др. представляют собой вязкоупругие или упруговязкие системы. Их свойства проявляются при действии внешней силы и можно продемонстрировать сочетанием упругих и вязких элементов. Упругие и вязкие свойства тел удобно моделировать. Это даёт возможность наглядно представить механические свойства биологических объектов. Примером модели упругого элемента является идеально упругая пружина (рис.3), в которой процесс деформации происходит мгновенно и подчиняется закону Гука: , (21)
, (21)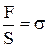 - напряжение; Е – модуль упругости, который численно равен приложенному напряжению, при котором длина образца удваивается;
- напряжение; Е – модуль упругости, который численно равен приложенному напряжению, при котором длина образца удваивается; 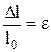 - относительное удлинение; Δl – изменение длины (абсолютное удлинение); l0 – исходная длина.
- относительное удлинение; Δl – изменение длины (абсолютное удлинение); l0 – исходная длина. Примером чисто вязкого элемента является цилиндр с вязкой жидкостью и неплотным поршнем (рис.4). Силу сопротивления среды в этом случае принимают пропорциональной скорости перемещения:
Примером чисто вязкого элемента является цилиндр с вязкой жидкостью и неплотным поршнем (рис.4). Силу сопротивления среды в этом случае принимают пропорциональной скорости перемещения:  .
. , (22)
, (22) где t – время действия; η – вязкость вещества.
где t – время действия; η – вязкость вещества.



 Три степени свободы имеет соединение, называемое «шаровой шарнир» (рис.10). Такое соединение осуществлено в тазобедренном суставе, в лопаточно-плечевом суставе. Шесть степеней свободы имеет череп, благодаря некоторой подвижности межпозвонковых суставов.
Три степени свободы имеет соединение, называемое «шаровой шарнир» (рис.10). Такое соединение осуществлено в тазобедренном суставе, в лопаточно-плечевом суставе. Шесть степеней свободы имеет череп, благодаря некоторой подвижности межпозвонковых суставов.
 , где F – действующая сила; R – сила преодолеваемого сопротивления; a и b – плечи сил. a>b тогда F<R. Примером является череп (рис.11а), ось вращения О которого проходит через сочленение черепа с первым позвонком, сила R – сила тяжести головы приложена несколько позади турецкого седла, действующая сила F – сила тяги мышц и связок, прикреплённых к затылочной кости.
, где F – действующая сила; R – сила преодолеваемого сопротивления; a и b – плечи сил. a>b тогда F<R. Примером является череп (рис.11а), ось вращения О которого проходит через сочленение черепа с первым позвонком, сила R – сила тяжести головы приложена несколько позади турецкого седла, действующая сила F – сила тяги мышц и связок, прикреплённых к затылочной кости. Второй вид рычага – рычаги скорости, в которых происходит выигрыш в скорости перемещения, но проигрыш в силе (рис.12). Условие равновесия этого рычага:
Второй вид рычага – рычаги скорости, в которых происходит выигрыш в скорости перемещения, но проигрыш в силе (рис.12). Условие равновесия этого рычага:  , а общая мощность
, а общая мощность  .
. (dx – величина укорочения мышцы за время dt).
(dx – величина укорочения мышцы за время dt). и qХ имеется определённое соотношение.
и qХ имеется определённое соотношение. Оказалось, что qХ не зависит от нагрузки Р, но зато всегда прямопропорционально величине укорочения x: qХ= а х, где а – постоянный для данной мышцы коэффициент, имеющий размерность силы (т.к. qХ – энергия, а х – путь). Во второй серии опытов Хилл исследовал зависимость между Р и
Оказалось, что qХ не зависит от нагрузки Р, но зато всегда прямопропорционально величине укорочения x: qХ= а х, где а – постоянный для данной мышцы коэффициент, имеющий размерность силы (т.к. qХ – энергия, а х – путь). Во второй серии опытов Хилл исследовал зависимость между Р и  , где b равно тангенсу угла наклона полученной прямой, а Р0=Р при
, где b равно тангенсу угла наклона полученной прямой, а Р0=Р при  . При этом величина находилась из опытов по определению теплопродукции мышцы. Физический смысл величины Р0 заключается в том, что при данной нагрузке укорочение мышцы не происходит, иными словами Р0 – это сила, развиваемая мышцей в изометрическом режиме сокращения (при х=0).
. При этом величина находилась из опытов по определению теплопродукции мышцы. Физический смысл величины Р0 заключается в том, что при данной нагрузке укорочение мышцы не происходит, иными словами Р0 – это сила, развиваемая мышцей в изометрическом режиме сокращения (при х=0). Наиболее распространённым в настоящее время техническим устройством, измеряющим работоспособность человека и нагрузку на сердце, является эргометр (рис.14), представляющий тормозной велосипед (велоэргометр). Здесь работа, совершаемая человеком, определяется по силе трения прижимного башмака 2, измеряемой динамометром 3. Динамометр может быть механическим или магнитным устройством.
Наиболее распространённым в настоящее время техническим устройством, измеряющим работоспособность человека и нагрузку на сердце, является эргометр (рис.14), представляющий тормозной велосипед (велоэргометр). Здесь работа, совершаемая человеком, определяется по силе трения прижимного башмака 2, измеряемой динамометром 3. Динамометр может быть механическим или магнитным устройством. . Полная работа за n оборотов, которые записывает счётчик, будет:
. Полная работа за n оборотов, которые записывает счётчик, будет: .
. .
.


