Расчет среднего и среднего квадратического отклонения
Тогда среднее квадратическое отклонение:
Коэффициент вариации:
Средняя численность работников промышленных предприятий региона составляет 2165 человек. Среднее квадратическое отклонение описывает абсолютный разброс значений показателя X и в данном случае составляет 703 чел. Коэффициент вариации характеризует относительный разброс признака вокруг среднего значения и составляет 32.46%. Определим моду по таблице 5. Модальный интервал – это тот, которому соответствует наибольшая частота (19 заводов). Следовательно, модальный интервал - это интервал с численность работающих от 2104 до 2548 человек. Для интервального ряда моду определим по формуле:
где х0 – нижняя граница модального интервала, то есть 2104 чел.; h – величина модального интервала (444 чел.); mМо – частота модального интервала (19); mМо-1 – частота интервала, предшествующего модальному (15); mМо+1 - частота интервала, следующего за модальным (15).
Найдем медиану, то есть значение признака, приходящееся на середину ранжированной совокупности. Определим ее по формуле:
где х0 – нижняя граница медианного интервала 2104 чел.); h – величина медианного интервала (444 чел.); mМ е – частота медианного интервала (19); SМe-1 – накопленная частота интервала, предшествующего медианному (36). Для установления медианного интервала необходимо определить накопленную частоту каждого последующего интервала до тех пор, пока она не превысит половины суммы накопленных частот (в нашем случае 40 заводов). Медианным является интервал с границами от 2104 до 2548 чел. (табл. 4).
Таким образом, мода равна 2155 человек, медиана – 2011 человек. 4. Определим общую численность промышленных предприятий (объем генеральной совокупности). Так как произведено 10% выборочное обследование и объем выборки составляет 80 предприятий, то N = 800. Определим среднюю ошибку выборки для выборочной средней:
Т. е. средняя ошибка выборочной средней составляет 74,55 чел. Определим коэффициент t для заданной доверительной вероятности 0.993. Из таблицы распределения нормального закона (прил.1) получаем t = 2,7. Найдем предельную ошибку выборки Тогда доверительный интервал для ожидаемой средней численности работников промышленных предприятий региона определяется неравенством: 2165,5 - 201,3 <
т. е. истинное значение генеральной средней находится в интервале от 1964 чел. до 2367 чел. 5. Определим выборочную долю предприятий, имеющих численность более 1600 человек. Суммируя численности предприятий в группах из таблицы 2, получим m = 59. Выборочная доля равна w = m / n = 59/80 = 0,74. Определим среднюю ошибку выборки для выборочной доли: т. е. средняя ошибка выборочной доли составляет 0,047. Определим коэффициент t для заданной доверительной вероятности 0,996 из приложения 1. Из таблицы распределения нормального закона получаем t = 2,9. Вычислим предельную ошибку выборки:
Тогда доверительный интервал для ожидаемой доли предприятий с численностью работников более 1660 чел. определяется неравенством: 0,74 – 0,14 < р < 0,74 + 0,14, 0,6 < р < 0,88. Таким образом, ожидаемая доля предприятий с численностью работников более 1600 человек находится в пределах от 0,6 до 0,88 или от 60% до 88%.
|



 = 702,88 чел.=703 чел.
= 702,88 чел.=703 чел.
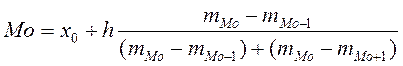 ,
,
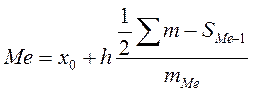 ,
,


 чел.
чел. < 2165,5 + 201,3
< 2165,5 + 201,3 ,
,




