При пересечении поверхности проецирующей плоскостью одна из проекций линии сечения проецируется на соответствующий след этой плоскости и поэтому является известной. Задача сводится к определению другой проекции линии сечения (табл. 7.4).
Таблица 7.4
Алгоритм построения линии сечения
наклонного конуса плоскостью
| Словесная форма
| Графическая форма
|
| 1. Точка 1 принадлежит фронтальному очерку конуса, точка 2 принадлежит основанию конуса, точка 1 – высшая, точка 2 – низшая.
Построить горизонтальные проекции точек 1 и 2: на горизонтальной плоскости построить крайнюю образующую, на которой лежит точка 1. Опустить перпендикуляр линии связи из точки 12 на данную образующую.
Опустить перпендикуляр из точки 22 до пересечения с контуром основания конуса
| 
|
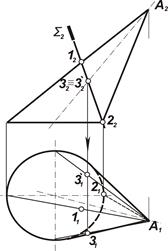
| 2. Отметить фронтально конкурирующие точки 3≡3΄ (32 ≡ 32΄), фронтальные проекции образующих, на которых лежат точки, совпадают с осью вращения конуса.
Построить горизонтальные проекции образующих и на них спроецировать горизонтальные проекции точек 31 и 31΄
| 
|
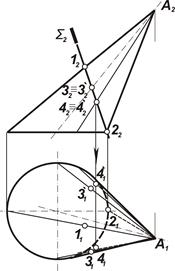
| 3. Точки 4 и 4΄ построить аналогично точкам 3 и 3΄.
Отметить проекции точек 42≡42΄, через отмеченные точки провести образующие, построить горизонтальные проекции образующих и на них отметить горизонтальные проекции точек 41 и 41΄
| 
|
Окончание табл. 7.4
| Словесная форма
| Графическая форма
|
| 4. Точки 5 и 6 принадлежат горизонтальным очеркам поверхности и являются точками границы видимости при проецировании конуса на плоскость П1.
Построить фронтальные проекции горизонтальных очерков и на пересечении этих линий с отрезком 1222 отметить проекции точек 52 и 62, затем найти горизонтальные проекции точек 51 и 61
| 
|
| 5. Соединить последовательно горизонтальные проекции полученных точек плавной кривой, участок линии 512161 – невидимый, так как располагается на невидимой части поверхности конуса
| 
|









