Усреднение вероятности реакции по ансамблю
Мы рассматривали отдельную молекулу с определенной энергией Е с одной степенью свободы – координатой реакции. На самом деле в эксперименте мы имеем дело с ансамблем частиц и измеряемая константа скорости реакции является усредненной по ансамблю. Введем Wn – вероятность частицы обладать энергией Еn, которая равна: Пусть td – время пребывания реагентов в зоне реакции, tr – время, необходимое для протекания химического акта. Последнее время складывается из времени электронной перестройки (tif), а также времени перехода из начального равновесного состояния в переходное и затем в конечное равновесное состояние. Время tr может быть велико, так что tr >> td. Это значит, реакция протекает в кинетическом режиме. В противоположном случае процессы контролируется диффузией, и скорости таких реакций мы уже рассматривали. При tr >> td большинство попаданий реагентов в реакционную зону не приводит к реакции. Благодаря частым неэффективным столкновениям реагентов с друг другом, с растворителем, со стенками функция распределения реагентов по энергии должна быть близка к равновесной, т.е. можно ожидать сохранения распределения Гиббса в ходе медленных, кинетически контролируемых реакций. Усредненная по ансамблю вероятность реакции равна:
Где первый множитель – вероятность реакции при энергии En, второй – вероятность обладать энергией En. Вероятность реакции
Как ведут себя
|

 , где F = -kTlnZ – свободная энергия Гельмгольца, Z – статсумма по всем состояниям. Встает вопрос – а справедливо ли распределение Гиббса если в системе идет химическая реакция?
, где F = -kTlnZ – свободная энергия Гельмгольца, Z – статсумма по всем состояниям. Встает вопрос – а справедливо ли распределение Гиббса если в системе идет химическая реакция? (12.1)
(12.1) при определенной энергии выражается так:
при определенной энергии выражается так: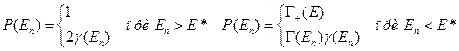
 при изменении энергии Е?
при изменении энергии Е?  . Поэтому существует некоторая оптимальная энергия
. Поэтому существует некоторая оптимальная энергия  , значение которой зависит от характера изменения
, значение которой зависит от характера изменения 


