Раздел II. Межмолекулярные взаимодействия и сольватация
Будем рассматривать 2 подхода: 1) Парные электростатические взаимодействия (ПЭВ 2) Взаимодействие растворенной частицы с континуальным растворителем Тема 3. Парные электростатические взаимодействия
В рамках первого подхода ПЭВ представим молекулу как Систему распределенных точечных зарядов и выпишем потенциал системы в удаленной точке на расстоянии R
При R >> ri мы можем разложить (3.1) в ряд:
В сферически симметричном случае
Единица измерения дипольного момента – 1 Дебай (10-18 ед. заряда СГС´см)
Напряженность поля диполя (F):
(так как дипольный момент – постоянный вектор, т.е. его проекции не зависят от координат)
Энергия взаимодействия зарядов
Пусть у нас два заряда: q1 и q2 на расстоянии r12. Если q1 закреплен, а q2 перемещается в бесконечность, то энергия взаимодействия есть работа сторонних сил по перемещению q2 против силы поля:
Примечание Следует различать полную энергию системы зарядов (3.3) и энергию i-го заряда во внешнем поле:
Энергия взаимодействия системы зарядов во внешнем поле Пусть j0 - потенциал внешнего поля, z1 – суммарный заряд системы точечных зарядов. Пренебрежем взаимодействием зарядов внутри системы, тогда можно представить энергию взаимодействия в виде:
Посчитаем теперь Е для разных случаев, считая что речь идет о взаимодействии 1 моля А с одним молем В. Ион-ион:
Итого, для пары положительный и отрицательный ион имеем
Ион-Диполь: Для удобства рассмотрим взаимодействия положительного заряда и диполя, лежащих на одной прямой на расстоянии R: + m2¾ - R + (z1e)
[m2] - в Дебаях (10-18 ед. заряда СГС´см), [Е] – в ккал/моль, [R]– ангстремы, [e] – в единицах СГСЭ
Если z1= 1, e = 5, а R = 3 А, m2 = 2 Дб, то Е = -3 ккал/моль.
Диполь-Диполь: +m1¾ - R + m2¾;- (ориентационное взаимодействие)
(*) – в случае, если диполи лежат на одной прямой
[m] - в Дебаях (10-18 ед. заряда СГС´см), [Е] – в ккал/моль, [R]– ангстремы
Если e = 5, а R = 3 А, m1 = m2 = 2 Дб, то Е = -0.8 ккал/моль, что сопоставимо с kT.
Индукционное взаимодействие
Поляризуемость [ a ] – возникновение в молекуле наведенного дипольного момента во внешнем электрическом поле: Посчитаем работу, затрачиваемую на наведение дипольного момента:
Размерность a - [cм3/молекула]. В свою очередь, наведенный дипольный момент взаимодействует с внешним полем: Оценим теперь данную энергию в зависимости от источника поля:
Ион А – поляризуемая молекула В:
Е [ккал/моль]; R – ангстремы, заряд – в единицах СГСЭ, a - [A3/молекула] Если e = 5, а R = 3 А, aB = 10 A3/молекула, zA = 1, то Е = -0.8 ккал/моль, что сопоставимо с kT.

FA лежит в плоскости, определяемой векторами mA и R. Поле Можно разложить на две компоненты, как показано на Рисунке.
Е [ккал/моль]; R – ангстремы, mA - в Дб, a - [A3/молекула] Если e = 5, а R = 3 А, aB = 10 A3/молекула, mA = 2 Дб, то Е = -0.03 ккал/моль, что много меньше kT. Однако, энергия взаимодействия с растворителем (концентрация 10 М) уже довольно существенна.
|


 (3.1)
(3.1)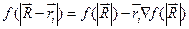 . Обозначим R =
. Обозначим R =  .
. , (
, ( ) тогда:
) тогда:
 (3.2)
(3.2) (3.3) - для дискретно распределенных зарядов (потенциал в данной формуле создается всеми зарядами, кроме i-го). Данная энергия состоит из 2-х частей: собственной энергии зарядов (которая вообще-то равна бесконечности, ибо заряды точечные) и энергии взаимодействия – которая только и имеет физический смысл.
(3.3) - для дискретно распределенных зарядов (потенциал в данной формуле создается всеми зарядами, кроме i-го). Данная энергия состоит из 2-х частей: собственной энергии зарядов (которая вообще-то равна бесконечности, ибо заряды точечные) и энергии взаимодействия – которая только и имеет физический смысл.

 , где
, где  , (e – заряд электрона)
, (e – заряд электрона) (3.4)
(3.4) (эрг/частица). Будем вычислять энергию и подставлять параметры в удобных величинах. Е [ккал/моль]; r12 – [ангстремы, СГС] = 10-8 (см, СИ), заряд – в единицах СГСЭ = 4.8´10-10 (Кулон, СИ). Тогда:
(эрг/частица). Будем вычислять энергию и подставлять параметры в удобных величинах. Е [ккал/моль]; r12 – [ангстремы, СГС] = 10-8 (см, СИ), заряд – в единицах СГСЭ = 4.8´10-10 (Кулон, СИ). Тогда:
 (3.5). Если │ z1│= │ z2│= 1, e = 5, а r12 = 3 А, то Е = -22 ккал/моль.
(3.5). Если │ z1│= │ z2│= 1, e = 5, а r12 = 3 А, то Е = -22 ккал/моль.
 (3.6)
(3.6) (*)
(*) (3.7)
(3.7) (в общем случае a - тензор, в частном - скаляр).
(в общем случае a - тензор, в частном - скаляр).
 . Таким образом, суммарный выигрыш в энергии за счет образования индуцированного диполя составляет
. Таким образом, суммарный выигрыш в энергии за счет образования индуцированного диполя составляет  .
. (3.8)
(3.8)

 (3.9)
(3.9)


