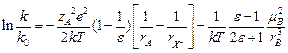Раздел IV. Кинетически-контролируемые реакции
Тема 10. Кинетически-контролируемые реакции в рамках теории активированного комплекса (ТАК)
Рассматриваем довольно медленные реакции, протекающие в кинетической области и мономолекулярные реакции, для которых не требуется сближение реагентов. Есть 2 подхода: 1) Теория переходного состояния (термодинамически равновесные условия). 2) Реакции в полярных растворителях при условии существенного перераспределения электронной плотности в реагентах (реакции переноса электрона и протона). Теория переходного состояния (активированного комплекса, ТАК):
Минимальный энергетический барьер между реагентами и продуктами. Переходное состояние – высшая (седловая) точка на многомерной поверхности потенциальной энергии. Седловая точка - точка, в которой потенциальная энергия максимальна при движении по одной из обобщенных координат и минимальна для всех остальных координат. В общем случае координата реакции – сложная суперпозиция расстояний и углов молекулярной системы. В простейших случаях (диссоциация) – координата реакции есть длина разрываемой связи.
Теория абсолютных скоростей реакции – была введена Эйрингом. Основное допущение и слабость теории – АК находятся в равновесии с реагентами. Предполагается, что если реакция пришла к равновесию, то реагенты и продукты в равновесии, значит и АК в равновесии. А теперь расширим это предположение на весь процесс. Но! Хотя мы и делаем сильное допущение, зато выигрываем в возможности рассчитать константу равновесия методами статистической термодинамики:
В случае линейного ротатора (s - число симметрии):
Если ротатор нелинейный:
Вывод связи между статсуммой и константой равновесия: A + B Û С ® продукт. Пусть (V,T) – const. В равновесии: dNA = dNB = - dNC = 0. Свободная энергия Гельмгольца имеет минимум:
Связь свободной энергии и статсуммы: F = - kTlnQ. Q = qN/N! для N частиц, q – статсумма 1 молекулы. Воспользуемся формулой Стирлинга – N!» (N/e)N.
Отсюда получаем, что: Учтем теперь разницу уровней отсчета энергии. Если считать колебательную энергию для каждой из потенциальных ям, то (10.1) надо умножить на exp(-E0/RT), где
Основные принципы теории абсолютных скоростей (или ТАК): (1) Статистическое Максвелл – Больцмановское распределение частиц в исходном и переходном состоянии. (2) Скорость химической реакции пропорциональна числу частиц в переходном состоянии. (3) Движение по координате реакции рассматривается как интенсивное колебание АК в направлении диссоциации на конечные продукты, причем hv < kT. В этих условиях можно представить (10.1) как:
Скорость реакции равна числу систем, проходящих в единицу времени через конфигурацию АК:
c - трансмиссионный коэффициент £ 1. Или еще
Тогда Если сопоставить это уравнение и уравнение Аррениуса
Влияние среды на константу скорости кинетически-контролируемых реакций. Будем работать в рамках ТАК. Рассмотрим реакцию: А + B Û X. Основное уравнение ТАК:
Будем считать, что в переходном состоянии реализуется не только минимум свободной энергии реагентов, но и свободной энергии растворителя. Влияние растворителя будем учитывать только через изменение свободной энергии реагентов и комплекса за счет сольватации. Механизм реакции будем считать неизменным.
Тогда можно записать, что
(А1) Реакция между ионами. Рассмотрим сближение двух ионов А и В с бесконечности на расстояние RAB.
(A2) Исходные реагенты и переходное состояние рассматриваются в виде заряженных проводящих шаров с радиусами rA, rB и rX и зарядами zA, zB и zX:
(В) Учет ионной силы.
В 1950 г. Девис и Ла-Мур провели исследование зависимости от I величин констант скорости 6-ти реакций между ионами и 2 реакций между ионами и нейтральными молекулами в воде. Было получено прекрасное согласие эксперимента и теории. Тангенс наклона зависимости Если теперь объединить результаты А2 и В, то можно записать:
Влияние растворителя на предэкспонент и энергию активации ионных реакций:
Оценим величину k0. k0 – нормальный предэкспонент, его можно представить как k0 = k1V*. k1 ~ n = 1013 c-1 (порядок частоты колебаний). V* = (r*)3 = (2´10-8)3 ~ 10-23 см3. Получим k0 = 10-10 см3/с ~ 6´1010 М-1с-1 – нормальное значение предэкспонента. Вспомним уравнение Аррениуса:
Влияние на энергию активации:
Полученное выражение объясняет часто наблюдаемый компенсационный эффект – одновременный рост предэкспонента и энергии активации, что приводит к тому, что суммарный эффект растворителя на константу скорости меньше, чем влияние по отдельности на A и Eact. Реакции дипольных молекул. Вспомним, что
Влияние среды на предэкспонент и энергию активации. Обозначим
Часто полагают, что
Часто вторым членом в
Рассмотрим теперь реакцию иона А в дипольной молекулой В. Переходное состояние у нас ион. Сольватация ионов – по Борну, диполя – по Кирквуду.
|

 Химическая реакция – плавное изменение конфигурации системы от исходного состояния в продукты реакции через переходное состояние (активированный комплекс).
Химическая реакция – плавное изменение конфигурации системы от исходного состояния в продукты реакции через переходное состояние (активированный комплекс). , где Qi – статсуммы, отнесенные к единице объема [см-3], Е0 – разность нулевых энергий продуктов и реагентов, ni - стехиометрический коэффициент. Покажем это:
, где Qi – статсуммы, отнесенные к единице объема [см-3], Е0 – разность нулевых энергий продуктов и реагентов, ni - стехиометрический коэффициент. Покажем это: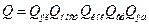 , квантовая статсумма
, квантовая статсумма  ,
,  - фактор вырождения. В классическом пределе (kT >> DE) можно от суммирования перейти к интегрированию. В этом приближении считаются
- фактор вырождения. В классическом пределе (kT >> DE) можно от суммирования перейти к интегрированию. В этом приближении считаются  и
и  . Для одномерного движения
. Для одномерного движения  . Для трехмерного
. Для трехмерного 

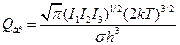 .
.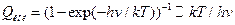 - для одного колебания.
- для одного колебания.

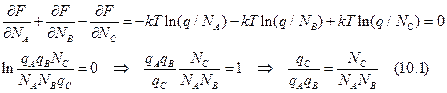
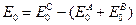 - разница нулевых энергий:
- разница нулевых энергий:  . Поделим на объем:
. Поделим на объем: 
 . Запишем теперь
. Запишем теперь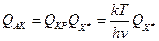 , где
, где  - статсумма АК за вычетом колебания вдоль КР.
- статсумма АК за вычетом колебания вдоль КР. , оценка дает
, оценка дает 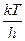 ~ 6´1012 с-1 при 300 К. Более употребительная формула:
~ 6´1012 с-1 при 300 К. Более употребительная формула:  , где
, где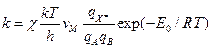 , где
, где 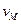 - молярный объем (~0.05 л/моль). Константа равновесия
- молярный объем (~0.05 л/моль). Константа равновесия  может быть записана как:
может быть записана как: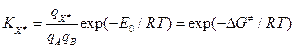 , где
, где  - свободная энергия активации – есть разность парциальной стандартной свободной энергии АК (с учетом отсутствия одной колебательной степени свободы) и суммой парциальных стандартных свободных энергий реагентов при концентрации 1 моль/л:
- свободная энергия активации – есть разность парциальной стандартной свободной энергии АК (с учетом отсутствия одной колебательной степени свободы) и суммой парциальных стандартных свободных энергий реагентов при концентрации 1 моль/л:  . Можно представить
. Можно представить 

 , то видно, что Е акт»
, то видно, что Е акт»  , а А =
, а А = 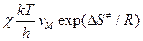 или
или  (кал´град-1´моль-1).
(кал´град-1´моль-1). (10.2)
(10.2)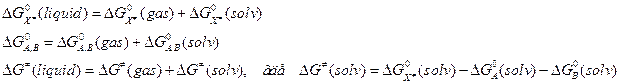
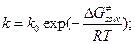 и если вспомнить, что
и если вспомнить, что  , то
, то  и
и 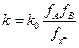 . Вопрос – как определить
. Вопрос – как определить  или
или  ? Нужны модельные представления.
? Нужны модельные представления.
 (10.3)
(10.3) . Вспомним формулу Борна:
. Вспомним формулу Борна:  :
: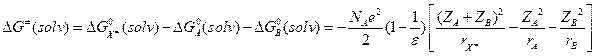
 (10.4) Модели А1 и А2 совпадают при rA = rB = rX.
(10.4) Модели А1 и А2 совпадают при rA = rB = rX.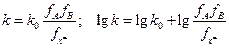 . В рамках приближения теории Дебая – Хюккеля:
. В рамках приближения теории Дебая – Хюккеля:  - ионная сила.
- ионная сила.  . Для воды, А = 0.51 (25 0С).
. Для воды, А = 0.51 (25 0С).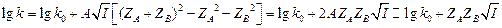 (10.5)
(10.5)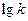 от
от  с экспериментальной точностью совпал с
с экспериментальной точностью совпал с 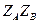 .
. (10.6)
(10.6)
 . Чему равно
. Чему равно  ? Рассмотрим модель А1:
? Рассмотрим модель А1: 
 В водных растворах с e = 80,
В водных растворах с e = 80, 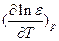 = - 0.0046. При RAB = 2 A,
= - 0.0046. При RAB = 2 A,  кал´моль-1´град-1.
кал´моль-1´град-1. 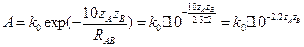 . Если
. Если  , то А = 103 М-1с-1, если
, то А = 103 М-1с-1, если 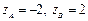 , то А = 1019 М-1с-1.
, то А = 1019 М-1с-1.
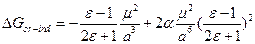 . Будем считать, что вторым членом можно пренебречь и
. Будем считать, что вторым членом можно пренебречь и  - Формула Кирквуда. Если нужно учесть и дисперсионные взаимодействия, то
- Формула Кирквуда. Если нужно учесть и дисперсионные взаимодействия, то 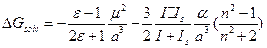 . Если брать
. Если брать  по Кирквуду, то
по Кирквуду, то 
 . Оценим порядок изменения константы скорости реакции при смене растворителя. Пусть e1 = 2, e2 = 80, mA=mB=0, mX = 5 D, rX = 5 А:
. Оценим порядок изменения константы скорости реакции при смене растворителя. Пусть e1 = 2, e2 = 80, mA=mB=0, mX = 5 D, rX = 5 А:
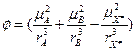
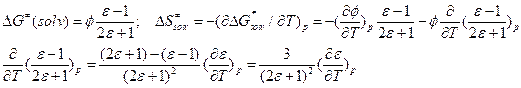
 , где l, s – некие константы. Такую зависимость наблюдают экспериментально.
, где l, s – некие константы. Такую зависимость наблюдают экспериментально. 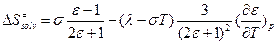 .
.
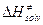 и
и 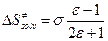 , а
, а  - опять наблюдаем компенсационный эффект!
- опять наблюдаем компенсационный эффект!