Что и т.д.
Посчитаем теперь
Вспомним, что
Считаем, что ионы точечные и интегрируем от нуля до бесконечности:
Запишем популярное выражение для электролита 1:1 при 250С в воде:
Данное выражение хорошо работает при I < 0.001. При более высоких ионных силах надо вводить поправки. Поправка №1. Снимаем условие о малости радиуса иона:
При высоких ионных силах вводится дополнительная поправка №2:
Недостатки теории Дебая – Хюккеля: 1. При решении уравнения Пуассона мы предполагали наличие Максвелл-Больцмановского распределения для зарядов, что вряд ли имеет место в реальности. 2. Взаимодействие между частицами определяется не только кулоновскими силой, но и Ван-дер-ваальсовыми силами и/или специфическими взаимодействиями. 3. Теория не работает в условиях, когда вещество плохо диссоциирует. (соли в неполярных растворителях).
Модель Онзагера – Бетчера (Сольватация дипольной молекулы)
В среде молекула растворенного вещества находится под воздействием всей совокупности окружающих молекул растворителя. В первом приближении можно считать, что полная энергия взаимодействия есть сумма парных взаимодействий:
В модели О-Б предполагается, что среда – это сплошной диэлектрический континуум. В этой среде рассматривается частица размером а и дипольным моментом
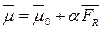 , где , где  – собственный дипольный момент, – собственный дипольный момент,  - поле, - поле,
появляющееся за счет поляризуемости среды внесенным диполем, наведенный дипольный момент.
Для вкладов ориентационных и индукционных взаимодействий в энергию сольватации можно написать следующее выражение:
(Энергия растяжения) (Энергия в-я диполя с полем) (Энергия поляризации среды полем) Откуда берется первое слагаемое? Мы растягиваем диполь на некоторое расстояние Х:
Формулу (3.20) можно переписать в другом виде:
Чему равно Частный случай – известная формула Кирквуда: Найдем теперь
Оценим теперь вклад каждого из трех слагаемых в свободную энергию сольватации, считая, что a = 2 А, a = 10 A3/молекула, I = 10 эВ, m = 2 Дб, e = 5, n2 = 2.
Раздел 3. Диффузионно – контролируемые реакции (ДКР) Тема 5. ДКР в рамках теории Смолуховского Начнем с рассмотрения вывода уравнения Смолуховского – уравнения, описывающего кинетику ДКР при равномерном начальном распределении реагентов. Предполагаем, что: 1) Реагенты находятся в тепловом равновесии 2) Задано равномерное начальное распределение веществ в пространстве 3) Движение молекул подчиняется уравнению макродиффузии (закон Фика) 4) Химическая реакция вводится как граничное условие на поверхности реагента
(А) Задача Смолуховского с «идеальным стоком»: A + B = C + B. Считаем, что концентрация частиц В (стоков) мала. Запишем:
В сферически-симметричном случае:
Покажем правильность тождества (4.2): Из уравнений (5.1) и (5.2) имеем: Вводим начальное и граничные условия: 1) 2) 3) При данном начальном и граничных условиях решение (5.3) имеет вид:
Убедимся, что это действительно решение: Примечание: Правило Лейбница
Проверим граничные и начальное условия:
 все сходится! все сходится!
Вычислим теперь полный поток (штук/с) частиц на сферу радиуса R:
при получаем стационарный поток Посчитаем, сколько частиц поглотит за время t « бесконечный сток»:
Подставим в (5.7) выражение (5.6) для W(t) и получим, что вероятность выжить есть:
Что такое
Таким образом, мы получили выражение для зависящей от времени константы скорости реакции А + В = В + С, т.е. в системе с постоянным числом стоков! Только при t >> R2/D мы получаем обычное значение А + А = С, то
граничное условие 3-рода Вместо граничного условия Смолуховского №2 (
Таким образом, наличие граничного условия 3-го рода обеспечивает нам появление двух стадий реакции – диффузионного сближения и реакции на контакте. Уравнение Смолуховского для вероятностей
то
Тема 6. Учет взаимодействия реагентов в уравнении Смолуховского
Делаем переход от концентраций к радиальной функции вероятности
Откуда берется второй член? Если есть потенциал взаимодействия, то есть и сила, отвечающая этому взаимодействию, которая в стационаре уравновешивается силой трения. При этом частица движется с постоянной скоростью v:
Дополнительный поток вероятности, связанный с U(r) равен: В сферически-симметричном случае: Константу скорости бимолекулярной реакции будем считать равной величине потока вероятности через поглощающую сферу радиуса R:
Используем граничное условие первого рода:
Введем обозначение
Решение однородного уравнения:
Решение: Соответственно, для диффузионной константы скорости получим:
Если у нас R << ROH, то Физический смысл радиуса Онзагера – расстояние, на котором энергия кулоновского взаимодействия сравнивается с тепловой энергией. Оценим эту величину для водного раствора, комнатной температуры и однозарядных реагентов:
Если ионы одного знака: Т.е. константа скорости резко падает по сравнению с диффузионной для нейтральных частиц. Оценим ее величину для водного раствора, комнатной температуры и однозарядных реагентов, R = 2 A: В случае произвольного центрально-симметричного потенциала: Где RD - по смыслу расстояние, на котором энергия взаимодействия равна тепловой.
Тема 7. Геминальная рекомбинация
Ранее была рассмотрена задача при равномерном начальном распределении реагентов. Однако, в фотохимии и радиационной химии частицы могут возникать парами, треками и т.д., т.е. неравномерно по пространству. Рассмотрим случай парного начального распределения. Пусть под действием импульса света у нас возникла пара радикалов на расстоянии r0. Процесс рекомбинации радикалов можно разделить на две части: геминальная рекомбинация в парах и рекомбинация в объеме, определяемая диффузией. Интерес представляет нахождение полной вероятности рекомбинации геминальной пары, либо наоборот – вероятности не вступить в реакцию. Постановка задачи: Уравнение Смолуховского (6.2) для радиальной функции вероятности.
Начальное условие:
Рассмотрим теперь предельные случаи: (1) Если у нас граничное условие 1 рода, т.е. скорость реакции на контакте равна бесконечности ( А) Рекомбинация незаряженных частиц: U(r) = 0, Б) q1q2< 0. Тогда вероятность геминальной рекомбинации C) q1q2> 0. Пусть у нас ROH >> R и ROH >> r0, тогда (2) Оставим граничное условие третьего рода, рекомбинация незаряженных частиц:
На самом деле частицы не рождаются на строго фиксированном расстоянии, всегда есть распределение по r0, такое что А) Несмещенное Гауссовское распределение: Б) Смещенное Гауссовское распределение: В) Экспоненциальное распределение:
Остановимся теперь на сравнении теории с экспериментальными результатами. Для нейтральных радикалов было получена формула (7.2). Если реализуется диффузионный контроль (
 )® N2 +R2 )® N2 +R2
Получено, что 1) Зависимость r0 от вязкости растворителя
Для рекомбинации атомов эта формула должна хорошо работать, т.к. вся избыточная энергия кванта идет в поступательную энергию. Однако, для многоатомных молекул это объяснение не годится, так как избыточная энергия уходит в основном на внутренние степени свободы и увеличение r0 с падением вязкости маловероятно. 2) Зависимость pR (h) связана с анизотропией реагентов. Мы всегда рассматривали реагенты как «черные» или «серые» сферы. Однако в реальности они скорее «белые» сферы с «черным» пятном. И вероятность рекомбинации зависит от геометрии взаимного расположения радикалов, т.е. насколько быстро они проворачиваются в клетке растворителя. Рассмотрим следующую модель: Радикалы рождаются развернутыми и угол разворота q~1/h. Решение задачи вращательной диффузии дает pR (q0)=(qа/q0)2, где qа – характерный размер пятна. Таким образом pR ~h2. Однако, выдвинутые предположения о причинах зависимости pR (h) пока не получили достаточной экспериментальной проверки, чтобы сделать однозначный вывод о правильности предложенных теоретических моделей. Тема 8. Учет анизотропии реагентов
Рассмотрим следующую модель: реакция изотропной частицы А с частицей В, на поверхности которой есть реакционный участок с телесным углом W0 - «белая сфера с черным пятном». Задача эквивалентна задаче о диффузии точечной частицы А к сфере радиусом RA+ RB и реакционным пятном на поверхности. Посчитаем площадь реакционной зоны:
Объем реакционной зоны: Для изотропных реагентов из решения уравнения Смолуховского было найдено, что среднее время пребывания частицы в реакционном слое t = RD/D. Используя этот факт, получим, что kD = Vr / t = 4pRD – правильное решение для изотропной задачи. В случае анизотропии реагентов kD = 4pR2D f /t и задача сводится к нахождению времени t. Оказалось, что время зависит от геометрического стерического фактора как
Тема 9. ДКР с дальнодействием
Процессы переноса энергии и электрона. В этом случае реакция вводится не как граничное условие, а входит в виде дополнительного члена в диффузионное уравнение. Начнем с рассмотрения процесса передачи энергии между донором (D) и акцептором (А):
Если оба электронных перехода А ® А* и D ® D* разрешены в дипольном приближении, то взаимодействием, приводящим к переносу энергии является диполь-дипольное взаимодействие. V ~ 1/r3. Вероятность передачи энергии по теории возмущений пропорциональна Если один из переходов запрещен по спину, то имеем обменное тушение Где k0 – константа скорости реакции на контакте, L - характерный параметр затухания волновых функций. Следует отметить, что в ходе всего процесса должен сохраняться полный спин системы.
Для начала рассмотрим задачу о затухании люминесценции в присутствии тушителя в жестких средах (матрицы) – в условиях, когда диффузией реагентов можно пренебречь. Пусть
Решение имеет вид
При выводе последней формулы мы совершили предельный переход N ® ¥,V ® ¥, CA = N/V = const. Тогда Если у нас тушение по диполь-дипольному механизму, то
Видно, что кинетика существенно неэкспоненциальна и собственно говоря, ввести понятие константы скорости нельзя. Вывод уравнения (9.1)
Случай обменного тушения (1) малые времена: k0t << 1 (2) большие времена: k0t >> 1 Т.е. на малых временах кинетика носит экспоненциальный характер и можно ввести эффективную константу скорости тушения Вывод формулы (9.2)
Вывод уравнения Штерн – Фольмера Так как он был в курсе лекций ВФП, то выводить не буду.
Перенос энергии в жидких растворах
На перенос энергии оказывает существенное влияние диффузия. Так как константа скорости убывает с расстоянием, то диффузия, приводящая к сближению реагентов, вызывает рост вероятности реакции. Запишем уравнение Смолуховского для вероятности нахождения донора в момент времени t на расстоянии r от акцептора. Где t0 – собственное время жизни донора, k(r) – константа скорости дистанционного тушения. Если ввести подстановку Введем граничное условие в общем виде (третьего рода):
1) Дополнительного тушения нет: 2) Решения уравнения (9.4) в общем случае нет. Но можно решить стационарную задачу:
Рассмотрим диффузионно-ускоренное тушение по диполь-дипольному механизму в случае В этом случае kst = 4pDReff, где Reff - сложная функция (Бесселя) безразмерного параметра 1) D ® ¥, U0 << 1, 2) D ® 0, U0 >> 1, Оценим параметры тушения в обычных жидкостях: R0 = 25 А, R = 5 А, D = 10-5 см2/с, t0 = 10-9 с Тогда Т.е. константа скорости тушения по диполь-дипольному механизму в 5 раз выше диффузионной. Рассмотрим тушение по обменному механизму в случае
1) D ® ¥, 2) D ® 0,
Краткое резюме по дистанционному тушению: 1) И для диполь-дипольного, и для обменного механизмов тушения возможен кинетический контроль, при этом
|

 Константу А легко найти в том случае, когда I = Iдобавки (т.е. при постоянной внешней ионной силе). При c®0 должен получаться потенциал точечного заряда
Константу А легко найти в том случае, когда I = Iдобавки (т.е. при постоянной внешней ионной силе). При c®0 должен получаться потенциал точечного заряда  . Отсюда
. Отсюда  (4.7)
(4.7)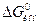 . Рассмотрим работу по созданию ионной атмосферы:
. Рассмотрим работу по созданию ионной атмосферы:
 , dА - работа по заряжению ионной атмосферы.
, dА - работа по заряжению ионной атмосферы.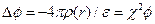 т.е.
т.е.  . Тогда:
. Тогда:

 . (4.8) Это выражение еще называют предельным законом Дебая – Хюккеля.
. (4.8) Это выражение еще называют предельным законом Дебая – Хюккеля.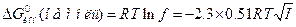
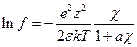 (4.9), где а – расстояние максимального сближения ионов. Формула (4.9) получается при интегрировании не от нуля, а от конечного размера а до бесконечности. Тогда:
(4.9), где а – расстояние максимального сближения ионов. Формула (4.9) получается при интегрировании не от нуля, а от конечного размера а до бесконечности. Тогда:
 , где С – эмпирическая константа
, где С – эмпирическая константа
 , равным:
, равным:
 -
-
 -энергия, затрачиваемая на создание полости в растворителе, в первом приближении не зависит от свойств молекулы, а определяется только размером полости и свойствами среды.
-энергия, затрачиваемая на создание полости в растворителе, в первом приближении не зависит от свойств молекулы, а определяется только размером полости и свойствами среды. (4.10)
(4.10)
 (4.11)
(4.11)

 , используя формулу Лондона:
, используя формулу Лондона:  . Рассчитаем энергию дисперсионного взаимодействия молекулы с молекулами растворителя, входящими в шаровой слой радиуса R и толщины dR (объем dV):
. Рассчитаем энергию дисперсионного взаимодействия молекулы с молекулами растворителя, входящими в шаровой слой радиуса R и толщины dR (объем dV): ,
,  - число молекул растворителя в шаровом слое объема dV = 4pR2dR. Подставим и проинтегрируем:
- число молекул растворителя в шаровом слое объема dV = 4pR2dR. Подставим и проинтегрируем: . Часто принимают, что
. Часто принимают, что  , тогда:
, тогда: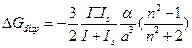 . Если мы теперь суммируем все сольватационные слагаемые:
. Если мы теперь суммируем все сольватационные слагаемые: (4.12)
(4.12)
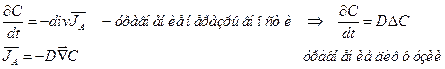 (5.1)
(5.1)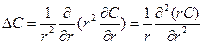 (5.2)
(5.2)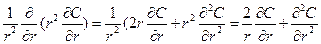 , с другой стороны:
, с другой стороны:  , что и т.д.
, что и т.д. (5.3).
(5.3). , при r > R, условие равномерного распределения реагента А при t = 0.
, при r > R, условие равномерного распределения реагента А при t = 0. , при t > 0 – условие реакции на поверхности стока В.
, при t > 0 – условие реакции на поверхности стока В. - сохранение начальной концентрации А на бесконечном удалении от стока В.
- сохранение начальной концентрации А на бесконечном удалении от стока В. (5.4)
(5.4)
 что и т.д.
что и т.д.

 , при распределении
, при распределении  .
. При этом мы считаем, что у нас V = ¥, N0 =¥, а N0/V = C0. Естественно, иметь дело с бесконечным числом частиц не хочется. Перейдем к вероятностной интерпретации: N0 =1, V = объем. Тогда N(t) – вероятность того, что за время t частица уйдет на сток. Обозначим эту вероятность за W(t).
При этом мы считаем, что у нас V = ¥, N0 =¥, а N0/V = C0. Естественно, иметь дело с бесконечным числом частиц не хочется. Перейдем к вероятностной интерпретации: N0 =1, V = объем. Тогда N(t) – вероятность того, что за время t частица уйдет на сток. Обозначим эту вероятность за W(t). (5.6) Нетрудно видеть, что данная величина безразмерна. Предположим, что данная величина много меньше единицы. Введем
(5.6) Нетрудно видеть, что данная величина безразмерна. Предположим, что данная величина много меньше единицы. Введем  - вероятность не погибнуть за время t на стоке. Если в объеме находится
- вероятность не погибнуть за время t на стоке. Если в объеме находится  стоков, где
стоков, где  - плотность стоков, то вероятность частицы А не погибнуть к моменту времени t есть:
- плотность стоков, то вероятность частицы А не погибнуть к моменту времени t есть:  (5.7)
(5.7) (5.8) - теперь предел вероятности выжить при t®¥; имеет физический смысл. Если в момент времени t = 0 было С0 частиц, то в момент времени t их будет
(5.8) - теперь предел вероятности выжить при t®¥; имеет физический смысл. Если в момент времени t = 0 было С0 частиц, то в момент времени t их будет  (5.9)
(5.9)
 (5.10)
(5.10) . Если у нас реакция:
. Если у нас реакция:
 (5.11) (мы фактически это делали ранее, приравнивали величину потока к скорости реакции на контакте). Рассмотрим решение стационарной задачи, в этом случае для любого r верно:
(5.11) (мы фактически это делали ранее, приравнивали величину потока к скорости реакции на контакте). Рассмотрим решение стационарной задачи, в этом случае для любого r верно:  (5.12) и
(5.12) и  . В этом случае решение уравнения (5.12) есть
. В этом случае решение уравнения (5.12) есть 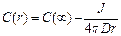 , откуда
, откуда  .
.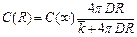 , вспомним, что мы выражали концентрацию частиц А:
, вспомним, что мы выражали концентрацию частиц А: (5.13)
(5.13)

 - плотность вероятности
- плотность вероятности - радиальная функция вероятности, если распределение равномерно,
- радиальная функция вероятности, если распределение равномерно, с другой стороны
с другой стороны 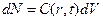 , отсюда:
, отсюда: 
 - связь между концентрацией реагента и радиальной функцией вероятности. Удобнее использовать
- связь между концентрацией реагента и радиальной функцией вероятности. Удобнее использовать 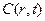 .
.
 (6.1)
(6.1)
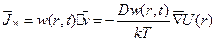
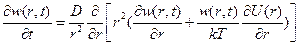 (6.2)
(6.2) (6.3)
(6.3) - это случай ДКР. Возьмем равномерное начальное распределение
- это случай ДКР. Возьмем равномерное начальное распределение  . Так как
. Так как  , то
, то  . Аналитического решения у временного уравнения нет, но можно найти стационарное решение:
. Аналитического решения у временного уравнения нет, но можно найти стационарное решение:  0. Пусть потенциал это Кулон:
0. Пусть потенциал это Кулон:  , тогда:
, тогда:
 - радиус Онзагера. Тогда в случае разноименных зарядов:
- радиус Онзагера. Тогда в случае разноименных зарядов:
 Это общее решение однородного уравнения. Частное решение неоднородного уравнения можно найти при
Это общее решение однородного уравнения. Частное решение неоднородного уравнения можно найти при  . Согласно математической теории, общее решение неоднородного уравнения есть сумма общего решения однородного плюс частное решение неоднородного уравнений.
. Согласно математической теории, общее решение неоднородного уравнения есть сумма общего решения однородного плюс частное решение неоднородного уравнений.  . Граничное условие:
. Граничное условие:


 - выражение для разноименных зарядов.
- выражение для разноименных зарядов.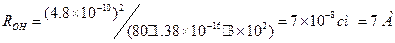 ; Если у нас R = 2 A, то получается, что константа скорости реакции будет в 4 раза выше, чем диффузионная для незаряженных частиц. Если у нас не вода, а неполярный растворитель с e = 2, то ROH = 250 А и константа скорости будет на пару порядков выше диффузионной!!
; Если у нас R = 2 A, то получается, что константа скорости реакции будет в 4 раза выше, чем диффузионная для незаряженных частиц. Если у нас не вода, а неполярный растворитель с e = 2, то ROH = 250 А и константа скорости будет на пару порядков выше диффузионной!! Решая это уравнение аналогично предыдущему, получим:
Решая это уравнение аналогично предыдущему, получим:  . При R << ROH
. При R << ROH 
 - на порядок меньше!!!
- на порядок меньше!!!


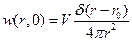 , нормировка
, нормировка  . Введем обозначения: r0 – расстояние в паре, R - реакционный радиус. Граничное условие на бесконечности:
. Введем обозначения: r0 – расстояние в паре, R - реакционный радиус. Граничное условие на бесконечности:  . Граничное условие третьего рода на поверхности реакционного радиуса:
. Граничное условие третьего рода на поверхности реакционного радиуса:  . Для решения (4.15) нужно использовать сложный аппарат функций Грина. Поэтому запишем только конечный результат для полной вероятности геминальной рекомбинации:
. Для решения (4.15) нужно использовать сложный аппарат функций Грина. Поэтому запишем только конечный результат для полной вероятности геминальной рекомбинации: (7.1) где
(7.1) где 
 ), тогда
), тогда  .
. . Таким образом, вероятность геминальной рекомбинации радикалов ~ 1/r0. Рекомбинация ион-радикалов:
. Таким образом, вероятность геминальной рекомбинации радикалов ~ 1/r0. Рекомбинация ион-радикалов:  .
. . Если у нас ROH >> R, то
. Если у нас ROH >> R, то 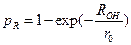 , если еще и ROH >> r0, то pR ~ 1.
, если еще и ROH >> r0, то pR ~ 1. .
. . Если у нас ROH = 7 А (вода), R = 3 А и r0 = 5 А, то pR = 0.33.
. Если у нас ROH = 7 А (вода), R = 3 А и r0 = 5 А, то pR = 0.33.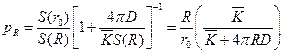 (7.2)
(7.2)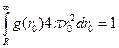 . Тогда мы должны усреднить pR по полному распределению:
. Тогда мы должны усреднить pR по полному распределению:  . Мы уже рассматривали один тип g(r0) – это d-функция. Есть и другие варианты (подробности см. в курсе ВФП «Радиационная химия»):
. Мы уже рассматривали один тип g(r0) – это d-функция. Есть и другие варианты (подробности см. в курсе ВФП «Радиационная химия»):
 , где s ~ 0.25 R, L – длина термализации электрона. Это распределение используется в радиационно-химических исследованиях.
, где s ~ 0.25 R, L – длина термализации электрона. Это распределение используется в радиационно-химических исследованиях.
 ), то
), то  и в первом приближении не зависит от вязкости. Если же наоборот
и в первом приближении не зависит от вязкости. Если же наоборот  , то
, то  , так как
, так как  . В общем случае
. В общем случае 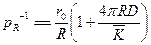 и
и  , что наблюдается экспериментально, например, при рекомбинации атомов йода и некоторых органических радикалов:
, что наблюдается экспериментально, например, при рекомбинации атомов йода и некоторых органических радикалов:  . Однако, в ряде случаев наблюдается зависимость от вязкости и для ДКР. Пример – фотолиз азодиизобутана:
. Однако, в ряде случаев наблюдается зависимость от вязкости и для ДКР. Пример – фотолиз азодиизобутана:
 . Наклон зависимости
. Наклон зависимости  равен 0.4. Отсюда можно определить отношение
равен 0.4. Отсюда можно определить отношение  (???). Однако из данных по объемной рекомбинации следует, что
(???). Однако из данных по объемной рекомбинации следует, что  . Объяснение наблюдаемого противоречия:
. Объяснение наблюдаемого противоречия: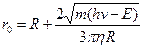 , где Е – пороговая энергия диссоциации. Откуда возникла эта формула? Пусть при поглощении кванта света у нас образовалось две частицы радиуса R/2, которые разлетаются с начальной скоростью v0 в разные стороны. Тогда по закону сохранения энергии:
, где Е – пороговая энергия диссоциации. Откуда возникла эта формула? Пусть при поглощении кванта света у нас образовалось две частицы радиуса R/2, которые разлетаются с начальной скоростью v0 в разные стороны. Тогда по закону сохранения энергии: 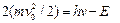
 . За счет трения в среде частицы будут тормозиться:
. За счет трения в среде частицы будут тормозиться: . Расстояние пройденное каждой частицей равно:
. Расстояние пройденное каждой частицей равно:  , где R – контактный радиус.
, где R – контактный радиус. (8.1)
(8.1) , где D - толщина реакционного слоя, а f – геометрический фактор. Далее, обозначим количество эффективных столкновений как Zeff и, предполагая, что отношение времени пребывания в зоне реакции (t) к времени свободного движения (1/ Zeff) равно отношению реакционного объема Vr к свободному объему Vf = 1/C. Тогда:
, где D - толщина реакционного слоя, а f – геометрический фактор. Далее, обозначим количество эффективных столкновений как Zeff и, предполагая, что отношение времени пребывания в зоне реакции (t) к времени свободного движения (1/ Zeff) равно отношению реакционного объема Vr к свободному объему Vf = 1/C. Тогда:  . Величина – Zeff/С по определению константа диффузионных встреч (kD). Таким образом, kD = Vr / t.
. Величина – Zeff/С по определению константа диффузионных встреч (kD). Таким образом, kD = Vr / t. , следовательно kD = 4pDReff (8.2), где
, следовательно kD = 4pDReff (8.2), где  . Т.е. все дело в перенормировке контактного радиуса и kD ~
. Т.е. все дело в перенормировке контактного радиуса и kD ~  .
.
 . Тогда k(r) ~
. Тогда k(r) ~ 
 - плотность частиц донора энергии D на расстоянии R1, R2 … RN от которых находится N акцепторов А. Тогда, для зависимости r от времени можно записать:
- плотность частиц донора энергии D на расстоянии R1, R2 … RN от которых находится N акцепторов А. Тогда, для зависимости r от времени можно записать: , где t0 – собственное время жизни донора.
, где t0 – собственное время жизни донора. . Предположим, что все молекулы по раствору распределены статистически равновероятно и усредним
. Предположим, что все молекулы по раствору распределены статистически равновероятно и усредним 

 , где R0 – Ферстеровский радиус (расстояние на котором константа тушения равна 1/ t0). Если пренебречь собственными объемами донора и акцептора можно вычислить:
, где R0 – Ферстеровский радиус (расстояние на котором константа тушения равна 1/ t0). Если пренебречь собственными объемами донора и акцептора можно вычислить: (9.1)
(9.1) , где
, где . Вспомним, что
. Вспомним, что  и найдем
и найдем  : Тогда нетрудно видеть, что
: Тогда нетрудно видеть, что 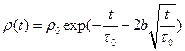 . Это можно проверить дифференцированием.
. Это можно проверить дифференцированием. . Результат в общем случае может быть получен только численным интегрированием. Рассмотрим предельные случаи:
. Результат в общем случае может быть получен только численным интегрированием. Рассмотрим предельные случаи: (9.2)
(9.2)
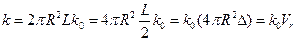 Т.е. фактически мы рассматриваем реакцию в тонком слое толщиной L/2. В случае обменного тушении понятие толщина реакционного слоя имеет ясный физический смысл – это характерный спад константы тушения в е раз.
Т.е. фактически мы рассматриваем реакцию в тонком слое толщиной L/2. В случае обменного тушении понятие толщина реакционного слоя имеет ясный физический смысл – это характерный спад константы тушения в е раз.


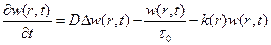 (9.3)
(9.3) .
.  (9.4)
(9.4) . Т.е. при контакте донора и акцептора включается дополнительный канал тушения с константой kC. В вышеуказанных условиях кинетика гибели доноров будет описываться следующим уравнением:
. Т.е. при контакте донора и акцептора включается дополнительный канал тушения с константой kC. В вышеуказанных условиях кинетика гибели доноров будет описываться следующим уравнением: , где первое слагаемое –обычный диффузионный член, второе – усреднение дистанционной константы. Можно вводить и другие варианты граничных условий:
, где первое слагаемое –обычный диффузионный член, второе – усреднение дистанционной константы. Можно вводить и другие варианты граничных условий: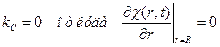 .
.
 (9.5)
(9.5) :
: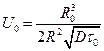 . R0 – Ферстеровский радиус, R - радиус контакта. Рассмотрим 2 предельных случая
. R0 – Ферстеровский радиус, R - радиус контакта. Рассмотрим 2 предельных случая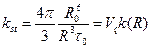 ; где
; где  – запрещенный объем.
– запрещенный объем. и т.к. U0 >> 1 то,
и т.к. U0 >> 1 то,  .
. , где
, где 
 .
. , где V – объем реакционного слоя.
, где V – объем реакционного слоя.
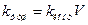 , (V – реакционный объем, k конт – константа скорости реакции на контакте) и диффузионный контроль, когда kтуш = 4pDReff,где Reff - сложная функция параметров тушения и коэффициента диффузии. Обратить внимание на универсальность формулы k = 4pDReff
, (V – реакционный объем, k конт – константа скорости реакции на контакте) и диффузионный контроль, когда kтуш = 4pDReff,где Reff - сложная функция параметров тушения и коэффициента диффузии. Обратить внимание на универсальность формулы k = 4pDReff


