Над алфавитом мощностью m можно создать ровно mn слов длиною n.
Доказательство:
Воспользуемся методом полной математической индукции. Пусть  - элементы (буквы) алфавита
- элементы (буквы) алфавита  мощностью
мощностью 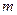 . Из этого алфавита можно создать
. Из этого алфавита можно создать 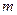 слов длиной 1. Такими словами будут буквы этого алфавита. Для
слов длиной 1. Такими словами будут буквы этого алфавита. Для  данное утверждение является правильным
данное утверждение является правильным  .
.
Допустим, что данное утверждение является правильным для 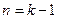 , и покажем, что тогда оно выполняется и для
, и покажем, что тогда оно выполняется и для 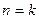 . Предположим, число длины
. Предположим, число длины  равняется
равняется 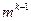 . Чтобы создать все возможные слова длины
. Чтобы создать все возможные слова длины 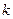 , достаточно к каждому слову длины
, достаточно к каждому слову длины  добавить в его конце последовательно каждую из
добавить в его конце последовательно каждую из 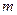 букв алфавита. Таким образом, из каждого слова длины
букв алфавита. Таким образом, из каждого слова длины  образуется
образуется 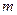 разных слов длины
разных слов длины 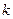 . Таким образом, получаем все возможные слова длиною
. Таким образом, получаем все возможные слова длиною 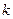 . Поскольку слов длиной
. Поскольку слов длиной  является
является 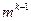 , то общее количество слов длиной
, то общее количество слов длиной 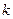 будет
будет  . Таким образом, предположив истинность утверждения для
. Таким образом, предположив истинность утверждения для 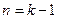 , доказано, что оно является правильным для
, доказано, что оно является правильным для 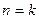 . Теорема доказана.
. Теорема доказана.
Пример 1.
Какой является мощность алфавита, с помощью которого записано сообщение, которое содержит 5120 символов, если его информационный объем составляет 2,5Кб?
1. Переведем информационный объем сообщения в биты:
 .
.
2. Определим количество битов, которые приходятся на один символ:
 .
.
3. Определяем мощность алфавита по теореме 1:


 - элементы (буквы) алфавита
- элементы (буквы) алфавита  мощностью
мощностью 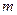 . Из этого алфавита можно создать
. Из этого алфавита можно создать  данное утверждение является правильным
данное утверждение является правильным  .
.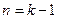 , и покажем, что тогда оно выполняется и для
, и покажем, что тогда оно выполняется и для 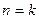 . Предположим, число длины
. Предположим, число длины  равняется
равняется 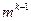 . Чтобы создать все возможные слова длины
. Чтобы создать все возможные слова длины 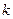 , достаточно к каждому слову длины
, достаточно к каждому слову длины  . Таким образом, предположив истинность утверждения для
. Таким образом, предположив истинность утверждения для  .
. .
.



