Измерение количества информации по Р.Хартли.
Меру количества информации установил в 1928 году Р.Хартли на основе предложенной им концепции выбора. Согласно этой концепции связь между отправителем и получателем информации осуществляется только при наличии определенного набора сообщений, из которых отправитель в каждый момент времени выбирает только одно. В результате последовательных выборов вниманию получателя предлагается последовательность сообщений (символов). Во время каждого выбора исключаются все другие сообщения (символы), которые могли бы быть выбраны. Пусть сообщение состоит из
Хартли установил, что в роли меры количества информации, которая имела бы практическую ценность, лучше выбрать не число
Мера количества информации, введенная Хартли, целиком согласуется с природными интуитивными требованиями к такой мере. Прежде всего, интуитивно ощущается, что количество информации в сообщении будет тем больше, чем длиннее сообщение: например, более длинная телеграмма содержит и больше сведений. Кроме этого, характеристика какого-нибудь явления будет тем лучше, чем большую разновидность сообщений о нем можно использовать. Например, оценка студента по 100-бальной системе лучше отражает его знания, чем пятибальная. Формула (1.3) отображает и зависимость количества информации от длины сообщения Пусть есть система где Поскольку в информационных процессах наиболее широко используется двоичная система счисления, то из практических соображений выбирают
где
Следовательно, тут бит не является наименьшей единицей измерения информации.
|

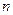 элементов, которые последовательно и независимо выбирают из
элементов, которые последовательно и независимо выбирают из 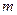 равновероятных элементов. Число возможных сообщений в этом случае (по теореме 1):
равновероятных элементов. Число возможных сообщений в этом случае (по теореме 1):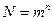 (1.3)
(1.3) , а логарифм этого числа:
, а логарифм этого числа: (1.4)
(1.4)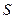 из
из  , то длину
, то длину  (1.5)
(1.5)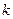 - коэффициент пропорциональности (масштабирования, зависимо от выбранной длины измерения),
- коэффициент пропорциональности (масштабирования, зависимо от выбранной длины измерения),  - основа системы меры,
- основа системы меры,  - количество информации, которую дает появление одного из
- количество информации, которую дает появление одного из  . Формулу Хартли рассматривают в виде:
. Формулу Хартли рассматривают в виде: (1.6)
(1.6) .
.



