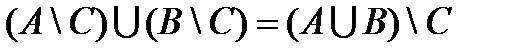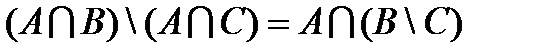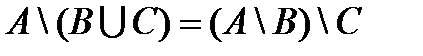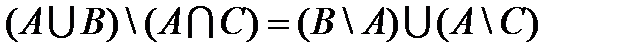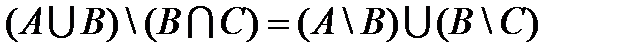Задачи 1-20
Доказать равенства, используя свойства операций над множествами.
Задачи 21-40
Пусть имеется множество A ={1,2,3,4}, на этом множестве определены отношения R Í A 2 и P Í A 2.
а) Определить, является ли отношение P рефлексивным.
б) Построить графические представления отношений R, P, P◦R.
в) Найти области определения и множества значений для отношений R, P, P◦R.
| Номер задачи
| Отношения R, P
| |
| R ={(x,y)| x 2 ³ 12 y }, P ={(x,y)| xy +1 делится на 3}
| |
| R ={(x,y)| x 2 £ 2 y }, P ={(x,y)| xy +1 делится на 3}
| |
| R ={(x,y)| x 2 ³ 3(x+y)}, P ={(x,y)| xy +1 делится на 3}
| |
| R ={(x,y)| x 2 £ 3(y-x)}, P ={(x,y)| xy +1 делится на 3}
| |
| R ={(x,y)| x 2 ³ 12 y }, P ={(x,y)| x +3 y делится на 4}
| |
| R ={(x,y)| x 2 £ 2 y }, P ={(x,y)| x +3 y делится на 4}
| |
| R ={(x,y)| x 2 ³ 3(x+y)}, P ={(x,y)| x +3 y делится на 4}
| |
| R ={(x,y)| x 2 £ 3(y-x)}, P ={(x,y)| x +3 y делится на 4}
| |
| R ={(x,y)| x 2 ³ 12 y }, P ={(x,y)| x + y2 делится на 3}
| |
| R ={(x,y)| x 2 £ 2 y }, P ={(x,y)| x + y2 делится на 3}
| |
| R ={(x,y)| x 2 ³ 3(x+y)}, P ={(x,y)| x + y2 делится на 3}
| |
| R ={(x,y)| x 2 £ 3(y-x)}, P ={(x,y)| x + y2 делится на 3}
| |
| R ={(x,y)| x 2 ³ 12 y }, P ={(x,y)| x2 +3 y делится на 4}
| |
| R ={(x,y)| x 2 £ 2 y }, P ={(x,y)| x2 +3 y делится на 4}
| |
| R ={(x,y)| x 2 ³ 3(x+y)}, P ={(x,y)| x2 +3 y делится на 4}
| |
| R ={(x,y)| x 2 £ 3(y-x)}, P ={(x,y)| x2 +3 y делится на 4}
| |
| R ={(x,y)| x 2 ³ 12 y }, P ={(x,y)| 2 x + y2 делится на 4}
| |
| R ={(x,y)| x 2 £ 2 y }, P ={(x,y)| 2 x + y2 делится на 4}
| |
| R ={(x,y)| x 2 ³ 3(x+y)}, P ={(x,y)| 2 x + y2 делится на 4}
| |
| R ={(x,y)| x 2 £ 3(y-x)}, P ={(x,y)| 2x+y2 делится на 4}
|
Задачи 41-60
Сколько четырехзначных чисел можно образовать из цифр указанного числа?
| Номер задачи
| Число
| Номер задачи
| Число
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Репродуктивное здоровье, как составляющая часть здоровья человека и общества
Репродуктивное здоровье – это состояние полного физического, умственного и социального благополучия при отсутствии заболеваний репродуктивной системы на всех этапах жизни человека...
Случайной величины Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
Понятие плотность распределения вероятностей случайной величины Х для дискретной величины неприменима...
Схема рефлекторной дуги условного слюноотделительного рефлекса При неоднократном сочетании действия предупреждающего сигнала и безусловного пищевого раздражителя формируются...
|
Толкование Конституции Российской Федерации: виды, способы, юридическое значение Толкование права – это специальный вид юридической деятельности по раскрытию смыслового содержания правовых норм, необходимый в процессе как законотворчества, так и реализации права...
Значення творчості Г.Сковороди для розвитку української культури Важливий внесок в історію всієї духовної культури українського народу та її барокової літературно-філософської традиції зробив, зокрема, Григорій Савич Сковорода (1722—1794 pp...
Постинъекционные осложнения, оказать необходимую помощь пациенту I.ОСЛОЖНЕНИЕ: Инфильтрат (уплотнение). II.ПРИЗНАКИ ОСЛОЖНЕНИЯ: Уплотнение...
|
|