Отношения на множествах
Бинарным отношением R на множествах А и В называется любое подмножество декартова произведения множеств А и В.
Если элементы x и y множеств А и В находятся в отношении R, то пишут (x,y)Î R или xRy. Если А = В, то R называется бинарным отношением на А. Бинарное отношение можно задать указанием всех элементов, входящих в соотношение, или графически. Основу графического представления бинарного отношения составляет прямоугольная система координат, где по одной оси откладываются элементы одного множества, а по второй – другого. Пересечения координат образуют точки, обозначающие элементы декартова произведения. Пример 1.2 Рассмотрим множества A ={1,2,3,4,5,6}, B ={1,2,3}. Определим на этих множествах отношение R Í A´B. R ={(x,y) | x делится на y }. R можно представить графически следующим образом:
Свяжем с каждым бинарным отношением R между множествами A и B два множества – область определения dR и множество значений rR. Они определяются следующим образом: dR ={ x | (x,y)Î R для некоторого y }, rR ={ y | (x,y)Î R для некоторого x }. Пример 1.3 Пусть на множестве A ={1,2,3,4,5} задано отношение R: R ={(x,y) | остаток от деления y на x равен 1}. Тогда R ={(5,1), (4,1), (3,1), (2,1), (2,3), (2,5), (3,4), (4,5)}, dR ={2,3,4,5}, rR ={1,3,4,5}. Пусть имеются множества A, B, C и отношения RÍA´B, PÍB´C. Определим отношение SÍA´C следующим образом: оно действует из A в B посредством R, а затем из B в C посредством P. Такое отношение называется составным и обозначается S=P◦R. S ={(x,y) | $ z Î B, для которого выполнено (x,z) ÎR, (z,y) ÎP }.
Пример 1.4 Пусть A ={1,2,3,4}, на множестве A определим два отношения: R ={(x,y) | 2x £ y } и P ={(x,y) | x+3y делится на 2}. Найдем графические представления отношений R, P, S = P◦R. Найдем области определения и области значений для всех отношений. dR ={1,2}, rR ={2,3,4}, dP ={1,2,3,4}, rP ={1,2,3,4}, dS ={1,2}, rS ={1,2,3,4}. Бинарное отношение R на множестве А называется рефлексивным, если для всякого Бинарное отношение R на множестве А называется симметричным, если из того, что выполняется xRy следует выполнение yRx. Бинарное отношение R на множестве А называется антисимметричным, если из выполнения xRy и yRx следует, что x=y. Бинарное отношение R на множестве А называется транзитивным, если из выполнения xRy и yRz следует выполнение xRz. Рефлексивное, симметричное и транзитивное отношение R на множестве A называется отношением эквивалентности. Рефлексивное, антисимметричное и транзитивное отношение R на множестве А называется частичным порядком. Пример 1.5. Определим отношение R на множестве натуральных чисел следующим образом: Это отношение является рефлексивным, т.к. Отношение R симметрично.
Отношение R не является антисимметричным, т.к. 6 R 3, 3 R 6, но Проверим, что R – транзитивно.
aRc выполнено.
|




 выполняется
выполняется  .
. (a+2b делится на 3).
(a+2b делится на 3).
 . Для того, чтобы проверить выполнение bRa, необходимо показать, что
. Для того, чтобы проверить выполнение bRa, необходимо показать, что 
 ,
, выполнено.
выполнено. .
.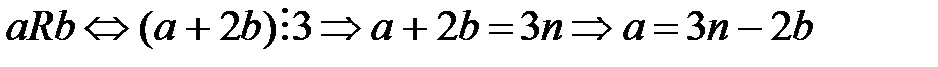 ,
, . Для того, чтобы проверить выполнение aRc, необходимо показать, что
. Для того, чтобы проверить выполнение aRc, необходимо показать, что 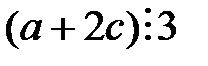 .
.