Формулы включений и исключений
Мощностью конечного множества называется количество элементов в нем. Если множество А имеет n элементов, то пишут Пусть имеется два пересекающихся множества А и В. Изобразим их на диаграмме Венна. Тогда имеет место следующая формула:
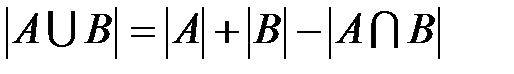
Для трех пересекающихся множеств выполняется:

Пример 2.9. В месяце было 12 дождливых, 8 ветреных, 4 холодных дня, дождливых и ветреных – 5, дождливых и холодных – 3, ветреных и холодных – 2, дождливых, ветреных и холодных – 1 день. Сколько дней была плохая погода? Пусть А – дождливые дни, В – ветреные дни, С – холодные, D – дни с плохой погодой. Тогда
В общем случае формула включений и исключений для k множеств
Пусть множество А состоит из N элементов и имеется n одноместных отношений (свойств)
Обобщая, получаем формулу, позволяющую вычислить число N (r) элементов, обладающих ровно r свойствами
Определим функцию [ x ] для вещественных чисел как наибольшее целое число, не превосходящее x. Число [ x ] называется целой частью числа x. Для положительных чисел а и b значение функции Пример 2.10. Сколько положительных трехзначных чисел делятся ровно на одно из чисел 3, 5 или 7? Обозначим P3 – свойство делимости на 3, P5 – на 5, P7 – на 7. Тогда
Так как N3,5 – число чисел, делящихся одновременно на 3 и 5, а наименьшее общее кратное 3 и 5 равно 15, то
|


 . Количество дней с плохой погодой:
. Количество дней с плохой погодой:
 имеет вид:
имеет вид: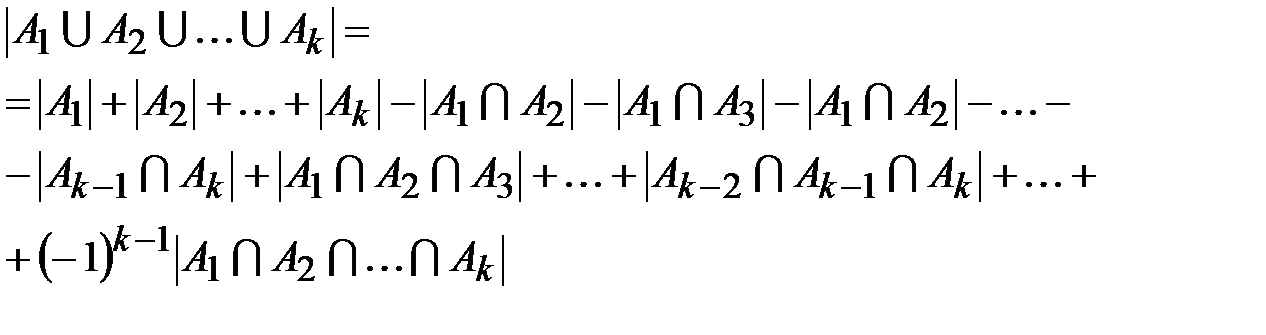
 . Каждый элемент множества может обладать или не обладать любым из этих свойств. Обозначим через
. Каждый элемент множества может обладать или не обладать любым из этих свойств. Обозначим через  число элементов, обладающих свойствами
число элементов, обладающих свойствами  и, может быть, некоторыми другими. Тогда число N (0) элементов, не обладающих ни одним из свойств
и, может быть, некоторыми другими. Тогда число N (0) элементов, не обладающих ни одним из свойств  , вычисляется по следующей формуле:
, вычисляется по следующей формуле: , где
, где
 .
. (1)
(1) равно количеству чисел из множества {1, 2,…, b }, которые делятся на а, т.е. кратны а.
равно количеству чисел из множества {1, 2,…, b }, которые делятся на а, т.е. кратны а.
 . Аналогично,
. Аналогично, 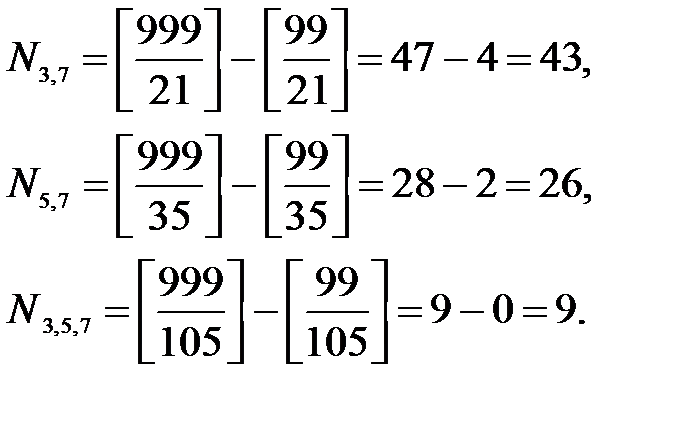
 По формуле (1) находим искомое число чисел:
По формуле (1) находим искомое число чисел:



