Нормальные формы
Булевы функции удобнее задавать в виде формул. Одной функции может соответствовать множество формул, содержащих аргументы функции, знаки дизъюнкции, конъюнкции и отрицания. Элементарной дизъюнкцией называется дизъюнкция конечного множества переменных или их отрицаний, в котором каждая переменная встречается не более одного раза. Пример 3.1. Элементарной конъюнкцией называется конъюнкция конечного множества переменных или их отрицаний, в котором каждая переменная встречается не более одного раза. Пример 3.2. Дизъюнктивной нормальной формой (днф) называется дизъюнкция конечного множества попарно различных элементарных конъюнкций. Пример 3.3. Аналогично, можно определить конъюнктивную нормальную форму (кнф), как конъюнкцию конечного множества попарно различных элементарных дизъюнкций. Пример 3.4. В примере видно, что Для любой функции можно найти ее представление в днф и кнф, используя аксиомы алгебры логики. Пример 3.5. Найти днф, кнф для функции
Любая булева функция может иметь много представлений в виде днф и кнф. Особое место среди этих представлений занимают совершенные днф (сднф) и совершенные кнф (скнф). Конституентой единицы k1 набора Пример 3.6. Построим СДНФ и СКНФ для функции f, для которой задана таблица истинности.
Для построения СДНФ рассмотрим все наборы, на которых функция принимает значение 1, и выпишем для этих наборов все k1:
Тогда СДНФ имеет вид:
Для построения СКНФ рассмотрим все наборы, на которых функция принимает значения 0, и выпишем для этих наборов k0:
Тогда СКНФ имеет вид:
Для построения СДНФ из ДНФ можно домножить элементарную конъюнкцию на Пример 3.7. Найти СДНФ для функции
Для построения СКНФ из КНФ в элементарную дизъюнкцию, не содержащую переменную xi, добавляем Пример 3.8. Найти СКНФ для функции В дальнейшем для представления СДНФ функции f будем указывать номера k1, на которых функция равна 1. Для определения набора необходимо перевести номер k1 в двоичное число. Пример 3.9. Пусть СДНФ функция f определяется следующим образом.
Переведем номера k1 в двоичные числа
Таким образом, f обращается в 1 на наборах (0,0,0,1), (0,1,0,1), (1,0,0,0), (1,0,1,1), (1,1,1,0). Аналогично, для представления функции в СКНФ будем использовать запись с указанием номеров k0, на которых функция равна 0. Пример 3.10. Переведем номера k0 в двоичные числа
Функция f обращается в 0 на наборах (0,0,1,0), (0,0,1,1), (0,1,1,1), (1,0,1,1).
|

 , x 1
, x 1 ,
, 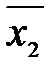
 ,
, 
 ,
, 
 является одновременно днф и кнф.
является одновременно днф и кнф.

 – Днф.
– Днф.

 – кнф.
– кнф. называется конъюнкция всех переменных, образующих этот набор. Причем, переменная входит в конъюнкцию с отрицанием, если она на данном наборе равна 0 и без отрицания, если она равна 1. Конституентой нуля k0 данного набора называется дизъюнкция всех переменных, образующих этот набор. Переменная входит в дизъюнкцию без отрицания, если она на этом наборе равна 0 и с отрицанием, если она равна 1. Совершенная дизъюнктивная нормальная форма функции f – дизъюнкция k1 тех наборов, на которых функция принимает значение 1. Совершенная конъюнктивная нормальная форма функции f – конъюнкция k0 тех наборов, на которых функция принимает значение 0. Представление функции в СДНФ или СКНФ единственно. Совершенные формы легко строить по таблице истинности.
называется конъюнкция всех переменных, образующих этот набор. Причем, переменная входит в конъюнкцию с отрицанием, если она на данном наборе равна 0 и без отрицания, если она равна 1. Конституентой нуля k0 данного набора называется дизъюнкция всех переменных, образующих этот набор. Переменная входит в дизъюнкцию без отрицания, если она на этом наборе равна 0 и с отрицанием, если она равна 1. Совершенная дизъюнктивная нормальная форма функции f – дизъюнкция k1 тех наборов, на которых функция принимает значение 1. Совершенная конъюнктивная нормальная форма функции f – конъюнкция k0 тех наборов, на которых функция принимает значение 0. Представление функции в СДНФ или СКНФ единственно. Совершенные формы легко строить по таблице истинности. ,
,  ,
,  ,
, 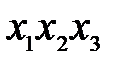 .
.
 ,
,  ,
, 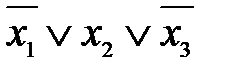 ,
,  .
.
 (если переменная xi отсутствует в элементарной конъюнкции) и применить закон дистрибутивности.
(если переменная xi отсутствует в элементарной конъюнкции) и применить закон дистрибутивности.

 – СДНФ.
– СДНФ. и применяем закон дистрибутивности.
и применяем закон дистрибутивности.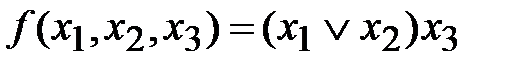

 – СКНФ.
– СКНФ. =
= 

 .
.



