Пусть G – помеченный граф с n вершинами и m ребрами. Определим матрицу смежности A(G) следующим образом:
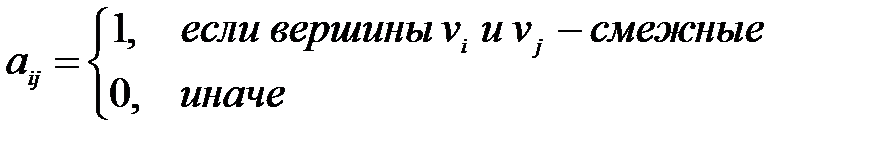
Матрица смежности квадратная, размера n ´ n.
Пример 4.5.
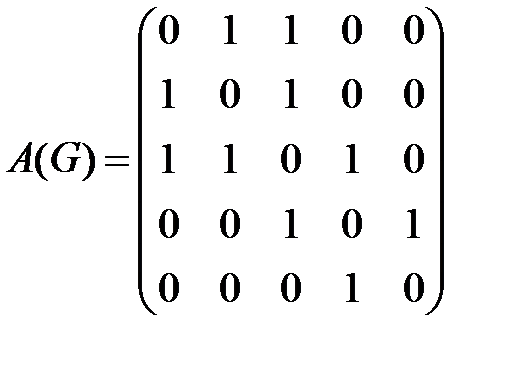
Можно заметить, что матрица смежности является симметричной, и количество единиц в каждой строке равно степени вершины, которой соответствует эта строка. По матрице смежности легко построить графическое представление графа.
Пример 4.6. Построить граф по матрице смежности

Можно определить матрицу инцидентности I(G), имеющую n строк и m столбцов, элементы которой задаются следующим образом:

Пример 4.7. Рассмотрим граф из примера 4.6, обозначив ребра.
e 1 
|
e 2 
|
e 3 
|
e 4 
|
e 7 
|
e 5 
|
e 6 
|

В каждой строке матрицы инцидентности только два элемента отличные от 0 (или один, если ребро является петлей). Поэтому такой способ описания оказывается неэкономным. Отношение инцидентности можно задать также списком ребер графа. Каждая строка этого списка соответствует ребру, в ней записаны номера вершин, инцидентных ему.
Пример 4.8. Рассмотрим граф из примера 4.7. Список ребер имеет вид:
 ,
, 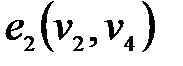 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
По списку ребер графа легко построить матрицу инцидентности, т.к. каждое ребро этого списка соответствует столбцу матрицы, а номера вершин в каждом элементе списка – это номера элементов строки матрицы инцидентности, которые равные 1.
Граф может быть представлен различными способами. Иногда не легко понять, одинаковы ли графы, изображенные разными чертежами или разными матрицами. Графы, отличающиеся только нумерацией вершин, называются изоморфными. Перенумерация задается строкой  новых номеров вершин, расположенных в исходном порядке. Новая матрица смежности получается в результате перемещения каждого элемента aij в
новых номеров вершин, расположенных в исходном порядке. Новая матрица смежности получается в результате перемещения каждого элемента aij в  строку и
строку и 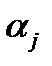 столбец, т.е. в результате перестановки (
столбец, т.е. в результате перестановки ( ) строк и столбцов исходной матрицы. Можно выполнить все возможные перестановки строк и столбцов для того, чтобы убедиться в неизоморфности графов, но это потребует n! перестановок, что достаточно трудоемко.
) строк и столбцов исходной матрицы. Можно выполнить все возможные перестановки строк и столбцов для того, чтобы убедиться в неизоморфности графов, но это потребует n! перестановок, что достаточно трудоемко.



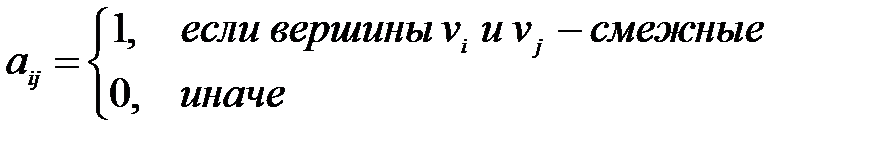



 ,
, 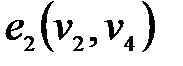 ,
,  ,
,  ,
,  ,
,  ,
,  .
. новых номеров вершин, расположенных в исходном порядке. Новая матрица смежности получается в результате перемещения каждого элемента aij в
новых номеров вершин, расположенных в исходном порядке. Новая матрица смежности получается в результате перемещения каждого элемента aij в  строку и
строку и 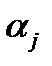 столбец, т.е. в результате перестановки (
столбец, т.е. в результате перестановки ( ) строк и столбцов исходной матрицы. Можно выполнить все возможные перестановки строк и столбцов для того, чтобы убедиться в неизоморфности графов, но это потребует n! перестановок, что достаточно трудоемко.
) строк и столбцов исходной матрицы. Можно выполнить все возможные перестановки строк и столбцов для того, чтобы убедиться в неизоморфности графов, но это потребует n! перестановок, что достаточно трудоемко.


