Минимизация конечных автоматов
Два автомата называются эквивалентными, если они для любой последовательности символов из входного алфавита X выдают одинаковую последовательность символов из выходного алфавита Y. Переход от автомата M к эквивалентному автомату называется эквивалентным преобразованием автомата M. Можно ставить много задач о поиске автоматов, эквивалентных данному и обладающих заданными свойствами. Наиболее изученной является задача о минимизации числа состояний автомата: среди всех автоматов, эквивалентных автомату M, найти автомат с наименьшим числом состояний (минимальный автомат). Пусть имеется автомат M=(Q, X, Y, d, l). Рассмотрим алгоритм Мили поиска минимального автомата. На каждом шаге алгоритма будем строить некоторое разбиение множества состояний Q на классы, причем разбиение на каждом шаге алгоритма будет получаться расщеплением некоторых классов предыдущего разбиения. Шаг 1. Два состояния q и q¢; относим в один класс C1j, если для каждого символа входного алфавита совпадают выходные символы для этих состояний, т.е. l(q, x)=l(q¢,x). Шаг i+1. Два состояния q и q¢; из одного класса Cij относим в один класс Ci+1,j, если для каждого символа входного алфавита осуществляется переход из состояний q и q¢; в состояния, принадлежащие одному и тому же классу Cis, т.е. d(q, x) и d(q¢,x) принадлежат одному и тому же классу. Если (i+1)-ый шаг не изменяет разбиения, то алгоритм заканчивается. Каждый класс соответствует состоянию минимального автомата. Пример 5.4. Построим минимальный автомат для автомата, заданного следующей таблицей переходов.
1, 3, 5, 6 и 2, 4. Шаг 2. Рассмотрим переходы в новые состояния для класса 1, 3, 5, 6 при входном символе 0: 1, 3, 5, 6 Состояния 3 и 5 принадлежат одному классу, а состояние 2 – другому. Следовательно, делаем разбиение класса 1, 3, 5, 6 на два новых класса: 1, 3, 5 и 6. После этого шага алгоритма имеем три класса: 1, 3, 5; 6 и 2, 4. Шаг 3. Рассмотрим переходы в новые состояния для класса 1, 3, 5 при входном символе 1: 1, 3, 5 Шаг 4. Рассмотрим переходы в новые состояния для класса 2, 4 при входном символе 0: 2, 4 Шаг 5. Рассмотрим переходы в новые состояния для класса 2, 4 при входном символе 1: 2, 4 Окончательно, разбиение на классы имеет вид: 1, 3, 5; 6; 2, 4. Таблица переходов минимального автомата будет иметь следующий вид:
Состоянию 1 минимального автомата соответствует класс 1, 3, 5, состоянию 2 – класс 6, состоянию 3 – класс 2, 4.
|

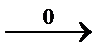 3, 5, 5, 2.
3, 5, 5, 2. 2, 2, 4. Так как состояния 2 и 4 находятся в одном классе, то нового разбиения на этом шаге не получим.
2, 2, 4. Так как состояния 2 и 4 находятся в одном классе, то нового разбиения на этом шаге не получим. 1, 5. Так как состояния 1 и 5 находятся в одном классе, то нового разбиения на этом шаге не получим.
1, 5. Так как состояния 1 и 5 находятся в одном классе, то нового разбиения на этом шаге не получим.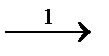 6, 6. Нового разбиения на этом шаге не получим.
6, 6. Нового разбиения на этом шаге не получим.


