Метод Квайна получения минимальной ДНФ
Процесс нахождения минимальной ДНФ из СДНФ можно разбить на следующие этапы: нахождение сокращенной ДНФ, нахождение всех тупиковых ДНФ, выбор из всех тупиковых минимальной ДНФ. Этап 1. Нахождение сокращенной ДНФ. Будем предполагать, что функция задана в СДНФ. Метод Квайна основан на том, что если выполнить в СДНФ все возможные неполные склеивания по формуле Пример 3.12. Результат склеивания наборов 0110 и 1110 – набор Х110, который соответствует импликанте Далее разобьем полученное множество импликант на группы по расположению X и произведем все возможные склеивания внутри каждой группы. Получим новое множество импликант для дальнейшего склеивания и, возможно, простые импликанты, не участвовавшие в склеивании. Склеивание продолжаем до тех пор пока, это возможно. Результат этого этaпа – построение всех простых импликант, т.е. сокращенной ДНФ. Этап 2. Нахождение минимальной ДНФ. По найденным на предыдущем этапе простым импликантам составляем импликантную таблицу, заголовки строк которой – простые импликанты, заголовки столбцов – K1 наборов из СДНФ. В таблице помечаем пересечение строки и столбца, если заголовок строки является импликантой заголовка столбца. Если в столбце имеется только одна метка, то импликанта, соответствующая этой строке, называется существенной, и она обязательно должна присутствовать в минимальной ДНФ. Включив эту импликанту в минимальную ДНФ, можно исключить из дальнейшего рассмотрения строку и все столбцы с пометками для этой импликанты. Если все пометки i -ой строки имеются также в j -ой строке, то j -я строка доминирует над i -ой, и i -ую строку можно исключить из дальнейшего рассмотрения. В частности, из рассмотрения исключаются строки без пометок. Если все пометки k -го столбца имеются также в m -ом столбце таблицы, то m-ый столбец доминирует над k -ым и m -ый столбец можно исключить из дальнейшего рассмотрения. Исключение существенных импликант, доминируемых строк и доминирующих столбцов проводят до тех пор, пока это возможно. Полученная после таких преобразований таблица называется циклической. Для выбора минимальной ДНФ в циклической таблице используют процедуру ветвления. Согласно алгоритму этой процедуры выбирают столбец с минимальным количеством пометок (таких столбцов может быть несколько) и для этих столбцов выбирают из строк, содержащих пометку в выбранном столбце, ту, которая содержит максимальное количество пометок и включают ее в минимальную ДНФ. После этого исключают строку, соответствующую найденной импликанте, и все помеченные в этой строке столбцы из дальнейшего рассмотрения. Если появилась строка, в которой во всех столбцах стоят пометки, то эту импликанту включают в минимальную ДНФ и на этом процесс нахождения минимальной ДНФ закончен. В противном случае выполняют преобразования для получения новой циклической таблицы. В результате описанных преобразований таблицы должны получить минимальную ДНФ. Пример 3.13. Найдем минимальную ДНФ для функции
Выпишем все наборы, на которых функция принимает значение 1.
Разобьем наборы на группы по количеству единиц. Первая группа состоит из наборов, не содержащих единиц: {0000}. Вторая группа состоит из наборов, содержащих одну единицу: {0100}. Третья группа состоит из наборов, содержащих две единицы: Выполним все возможные склеивания между элементами соседних групп, помечая наборы, участвующие в склеивании.
Результаты склеивания – импликанты, являющиеся K1 для наборов 0Х00, 01Х0, 0Х11, 011Х, Х110, Х111, 111Х. Импликанта, являющаяся K1 для набора 1001 – простая. Разобьем все полученные в результате склеивания импликанты по положению Х на группы. 1-я группа: 2-я группа: 3-я группа: 4-я группа: Произведем все возможные склеивания внутри каждой группы, помечая наборы, участвующие в склеивании.
Результат склеивания – импликанта, соответствующая X11X, и набор простых импликант, соответствующих 0Х00, 0Х11, 01Х0. Дальнейшее склеивание осуществить нельзя, поэтому Х11Х соответствует простой импликанте. Можно переходить к составлению импликантной таблицы.
Импликанты, соответствующие 0Х00, 0Х11, 1001, X11X – существенные, поэтому они обязательно входят в минимальную ДНФ. Удалим строки и столбцы для этих импликант из таблицы. Вычеркнутся все столбцы, следовательно, на этом процесс поиска минимальной ДНФ закончен. Минимальная ДНФ имеет следующий вид:
|

 , а затем все поглощения по формуле
, а затем все поглощения по формуле 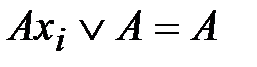 , где А – элементарная конъюнкция, то получим сокращенную ДНФ. Для удобства выполнения операции склеивания представим все k1 для наборов из СДНФ в виде их двоичных номеров и разобьем номера на группы по количеству единиц. Склеивание возможно между элементами соседних групп. Элементы, участвующие в склеивании будем помечать *. Результат склеивания – набор импликант и, возможно, простые импликанты, не отмеченные символом *. Для наборов, соответствующих импликантам, на месте отсутствующей переменной будем писать знак X.
, где А – элементарная конъюнкция, то получим сокращенную ДНФ. Для удобства выполнения операции склеивания представим все k1 для наборов из СДНФ в виде их двоичных номеров и разобьем номера на группы по количеству единиц. Склеивание возможно между элементами соседних групп. Элементы, участвующие в склеивании будем помечать *. Результат склеивания – набор импликант и, возможно, простые импликанты, не отмеченные символом *. Для наборов, соответствующих импликантам, на месте отсутствующей переменной будем писать знак X.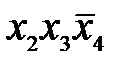 .
. =
=  .
.
 . Четвертая группа состоит из наборов, содержащих три единицы:
. Четвертая группа состоит из наборов, содержащих три единицы:  . Пятая группа состоит из наборов, содержащих четыре единицы: {1111}.
. Пятая группа состоит из наборов, содержащих четыре единицы: {1111}.









