Этот метод используется для формул с малым числом переменных. Карта Карно для функции n переменных содержит 2 n ячеек, каждая из которых соответствует одной из 2 n возможных комбинаций значений n булевых переменных x 1, x 2, …, xn. Две соседние ячейки отличаются значением только одной переменной. В случае функции трех переменных карту Карно можно представить в следующем виде:
Все ячейки, отмеченные скобкой
xi (по строке и столбцу), представляют наборы с
xi =1, а в неотмеченных строках и столбцах ячейки соответствуют наборам с
xi =0.
В случае четырех переменных карта Карно имеет следующий вид:
Булева функция может быть представлена на карте Карно выделением на карте ячеек, соответствующих наборам, на которых функция принимает значение 1. В этих ячейках будем писать 1. Незаполненные ячейки соответствуют нулям функции.
Пример 3.14. Заполним карту Карно для функции

2 k соседних ячеек, содержащие единицы, называются покрытием в том случае, если они расположены в виде прямоугольника или квадрата. При этом считается, что ячейки на противоположных концах строки или столбца являются соседними, как будто карта расположена на торе. Каждое покрытие соответствует импликанте. Покрытие, состоящее из двух ячеек, соответствует произведению всех переменных кроме одной, значением которой отличаются эти ячейки. Покрытие из четырех ячеек соответствует произведению, в котором отсутствуют две переменные и т.д. Чем больше ячеек в покрытии, тем проще импликанта. Для получения простой импликанты выбирается покрытие наибольшего размера.
Для построения минимальной ДНФ по карте Карно следуют двум правилам.
1. Выбирают покрытия наибольшего размера, содержащие ячейки, которые не могут быть ни в каком другом покрытии.
2. Для оставшихся ячеек выбирают покрытие наибольшего размера.
Пример 3.15. Найдем минимальную ДНФ для функции.
 =
= 
Выпишем двоичные номера всех K1:
0000, 0001, 0010, 0011, 0100, 0110, 0111, 1000, 1001, 1011, 1111.
Построим карту Карно и покроем все единицы на карте Карно покрытиями наибольшего размера.
Порядок построения минимальной ДНФ будет таким:
- Выбираем покрытие наибольшего размера для ячейки, соответствующей x 1 x 2 x 3 x 4. Это будет импликанта x 3 x 4.
- Выбираем покрытие для ячейки  . Это будет импликанта
. Это будет импликанта  .
.
- Выбираем покрытие для ячейки  . Это будет импликанта
. Это будет импликанта  .
.
Больше непокрытых ячеек не осталось, следовательно, минимальная ДНФ имеет вид 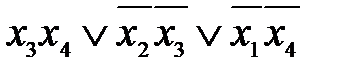 .
.


 =
= 
 . Это будет импликанта
. Это будет импликанта  .
. . Это будет импликанта
. Это будет импликанта  .
.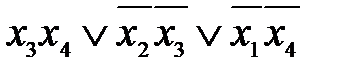 .
.


