Рекуррентные соотношения. Возвратные последовательности
Рекуррентным соотношением называется соотношение вида Пример 2.11. Формула Последовательность Пример 2.12. Геометрическая прогрессия – это возвратная последовательность, так как Многочлен Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим решением. Описание общего решения имеет аналоги с описанием решения обыкновенного дифференциального уравнения с постоянными коэффициентами. Пусть l – корень характеристического уравнения. Тогда общее решение рекуррентного соотношения можно найти следующим образом: 1. если li – корень кратности 1 (i =1,…, k), то общее решение имеет вид 2. если li – корень кратности ri (i =1,…, k), то общее решение имеет вид Зная общее решение рекуррентного соотношения, по начальным условиям можно найти неопределенные постоянные и тем самым получить частное решение рекуррентного уравнения с данными начальными условиями. Пример 2.13. Найти последовательность { an }, удовлетворяющую рекуррентному соотношению Составим характеристический многочлен Для нахождения корней сгруппируем слагаемые Составим характеристическое уравнение
решая которую находим с1 =1, с2 = 1, с3 =1. Таким образом,
|

 , которое позволяет вычислить все члены последовательности
, которое позволяет вычислить все члены последовательности  , если заданы ее первые k членов.
, если заданы ее первые k членов. задает арифметическую прогрессию.
задает арифметическую прогрессию.
 называется возвратной, если для всех n и некоторого k выполняется
называется возвратной, если для всех n и некоторого k выполняется  где pi = const.
где pi = const. . Следовательно, выполняется
. Следовательно, выполняется 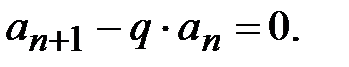
 называется характеристическим для возвратной последовательности.
называется характеристическим для возвратной последовательности. где ci = const (i =1,…, k).
где ci = const (i =1,…, k). , где
, где 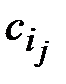 – произвольные константы (i =1,…, n, j =1,…, ri).
– произвольные константы (i =1,…, n, j =1,…, ri).

 .
. Его корнями являются числа
Его корнями являются числа  . Следовательно, общее решение рекуррентного соотношения имеет вид:
. Следовательно, общее решение рекуррентного соотношения имеет вид:  . Используя начальные условия, получим систему:
. Используя начальные условия, получим систему:
 .
.


