Выборки с повторениями
Размещениями с повторениями из n элементов по m называются упорядоченные выборки из m элементов множества, в которых элементы множества могут повторяться. Количество всех размещений с повторениями обозначим
Пример 2.4. Сколько всего трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?
Сочетаниями с повторениями из n элементов по m называются неупорядоченные выборки из m элементов множества, в которых элементы множества могут повторяться. Число всех сочетаний с повторениями обозначим
Пример 2.5. Сколько различных вариантов количества очков может выпасть при бросании двух кубиков?
Перестановками с повторениями из n элементов по k называется упорядоченная выборка из k элементов множества, в которой каждый элемент множества встречается ki раз (причем, k1+k2+... +kn=k). Число перестановок с повторениями обозначается
Пример 2.6. Сколько разных слов можно образовать при перестановке букв слова «математика»? В слове «математика» буква «м» встречается 2 раза, «а» – 3 раза, «т» – 2 раза, «е» – 1 раз, «и» – 1 раз, «к» – 1 раз. Поэтому число различных слов равно
При подсчете числа комбинаций используют два правила: правило суммы и правило произведения. Правило суммы. Если объект А можно выбрать m способами, а объект B – k способами, то объект «либо А, либо В» можно выбрать m+k способами. Правило произведения. Если объект А можно выбрать m способами, а после каждого такого выбора объект В можно выбрать k способами, то пару объектов А и В можно выбрать m×k способами. Пример 2.7. Сколько разных четырехзначных чисел можно составить из цифр 0, 1, 2? Из цифр 0, 1, 2 можно составить Пример 2.8 Сколько различных пятизначных чисел можно составить из цифр числа 1111222345600? Разделим все составленные числа на группы по первой цифре в числе. Таких групп будет три. 1-я группа. У чисел из этой группы на первом месте стоит «единица». Эти числа имеют вид 1****, где на место **** выбираются 4 цифры из набора 111222345600. Перечислим все возможные случаи. Это могут быть либо 3 «единицы» и любая цифра из множества {2,3,4,5,6,0}, либо 2 «единицы» и 2 «двойки», либо 2 «единицы» и 2 «нуля», либо 2 «единицы» и 2 любые цифры из множества {2,3,4,5,6,0}, либо 3 «двойки» и любая цифра из множества {1,3,4,5,6,0}, либо 2 «двойки» и 2 «нуля», либо 2 «двойки» и 2 любые цифры из множества {1,3,4,5,6,0}, либо 2 «нуля» и 2 любые цифры из множества {1,2,3,4,5,6}, либо 4 любые цифры из множества {1,2,3,4,5,6,0}. Всего таких чисел будет:
N = n1 + n2 + n3 =1446+1423+3116=5985.
|

 .
.
 .
.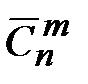 .
.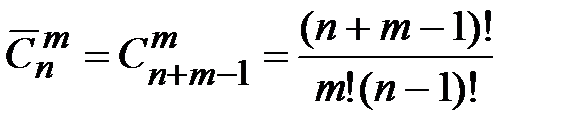
 .
.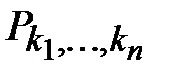


 число, но сюда входят числа, у которых первая цифра нуль, которые не являются четырехзначными. Таких чисел будет
число, но сюда входят числа, у которых первая цифра нуль, которые не являются четырехзначными. Таких чисел будет  . Поэтому ответ 81 – 27 = 54.
. Поэтому ответ 81 – 27 = 54. 2-я группа. У чисел из этой группы на первом месте стоит «двойка». Эти числа имеют вид 2****, где на место **** выбираются 4 цифры из набора 111122345600. Перечислим все возможные случаи. Это могут быть либо 4 «единицы», либо 3 «единицы» и любая цифра из множества {2,3,4,5,6,0}, либо 2 «единицы» и 2 «нуля», либо 2 «единицы» и 2 «двойки», либо 2 «единицы» и 2 любые цифры из множества {2,3,4,5,6,0}, либо 2 «двойки» и 2 «нуля», либо 2 «двойки» и 2 любые цифры из множества {1,3,4,5,6,0}, либо 2 «нуля» и 2 любые цифры из множества {1,2,3,4,5,6}, либо 4 любые цифры из множества {1,2,3,4,5,6,0}. Всего таких чисел будет:
2-я группа. У чисел из этой группы на первом месте стоит «двойка». Эти числа имеют вид 2****, где на место **** выбираются 4 цифры из набора 111122345600. Перечислим все возможные случаи. Это могут быть либо 4 «единицы», либо 3 «единицы» и любая цифра из множества {2,3,4,5,6,0}, либо 2 «единицы» и 2 «нуля», либо 2 «единицы» и 2 «двойки», либо 2 «единицы» и 2 любые цифры из множества {2,3,4,5,6,0}, либо 2 «двойки» и 2 «нуля», либо 2 «двойки» и 2 любые цифры из множества {1,3,4,5,6,0}, либо 2 «нуля» и 2 любые цифры из множества {1,2,3,4,5,6}, либо 4 любые цифры из множества {1,2,3,4,5,6,0}. Всего таких чисел будет: 3 -я группа. У чисел из этой группы на первом месте стоит ни «единица», ни «двойка», ни «нуль», т.е. одна из цифр множества {3,4,5,6}. Первую цифру можно выбрать 4 способами. Оставшиеся 4 цифры выбираются из набора 1111222345600 с учетом того, что одна из цифр множества {3,4,5,6} уже выбрана. Перечислим все возможные случаи. Это могут быть либо 4 «единицы», либо 3 «единицы» и любая цифра из множества {2,3,4,5,6,0}, либо 2 «единицы» и 2 «двойки», либо 2 «единицы» и 2 «нуля», либо 2 «единицы» и 2 любые цифры из множества {2,3,4,5,6,0}, либо 3 «двойки» и любая цифра из множества {1,3,4,5,6,0}, либо 2 «двойки» и 2 «нуля», либо 2 «двойки» и 2 любые цифры из множества {1,3,4,5,6,0}, либо 2 «нуля» и 2 любые цифры из множества {1,2,3,4,5,6}, либо 4 любые цифры из множества {1,2,3,4,5,6,0}. Всего таких чисел будет:
3 -я группа. У чисел из этой группы на первом месте стоит ни «единица», ни «двойка», ни «нуль», т.е. одна из цифр множества {3,4,5,6}. Первую цифру можно выбрать 4 способами. Оставшиеся 4 цифры выбираются из набора 1111222345600 с учетом того, что одна из цифр множества {3,4,5,6} уже выбрана. Перечислим все возможные случаи. Это могут быть либо 4 «единицы», либо 3 «единицы» и любая цифра из множества {2,3,4,5,6,0}, либо 2 «единицы» и 2 «двойки», либо 2 «единицы» и 2 «нуля», либо 2 «единицы» и 2 любые цифры из множества {2,3,4,5,6,0}, либо 3 «двойки» и любая цифра из множества {1,3,4,5,6,0}, либо 2 «двойки» и 2 «нуля», либо 2 «двойки» и 2 любые цифры из множества {1,3,4,5,6,0}, либо 2 «нуля» и 2 любые цифры из множества {1,2,3,4,5,6}, либо 4 любые цифры из множества {1,2,3,4,5,6,0}. Всего таких чисел будет: Всего пятизначных чисел будет:
Всего пятизначных чисел будет:


