Минимизация булевых функций в классе ДНФБудем получать выражение для булевой функции в виде ДНФ с минимальным числом вхождений переменных. Будем предполагать, что функция представлена в СДНФ. Элементарная конъюнкция называется импликантой Пример 3.11. Найдем импликанты и простые импликанты для функции
Из таблиц истинности заключаем, что Дизъюнкция всех простых импликант называется сокращенной ДНФ. Сокращенная ДНФ может содержать лишние импликанты, удаление которых не меняет таблицу истинности. При удалении из сокращенной ДНФ всех лишних импликант получаем тупиковую ДНФ. Выбор из всех тупиковых ДНФ формулы с наименьшим числом вхождений переменных дает минимальную ДНФ. Известны аналитические и графические способы построения минимальной ДНФ.
|
, если она равна 0 на тех наборах, на которых f обращается в 0. Простой импликантой называется импликанта, в которой отбрасывание любой буквы ведет к получению элементарной конъюнкции, которая не является импликантой.
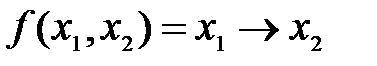. Всего имеется 8 элементарных конъюнкций с переменными x 1, x 2. Приведем их таблицы истинности.
, 
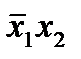
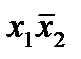
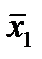
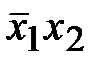, x 1 x 2, 
, x 2 являются импликантами функции f. Из них простыми являются 
и x 2.
