Тақырып. Мультиколлинеарлық.
Мысал. 20 жұмысқер бойынша толем ақы у (ақша бірліктері), жас шамасы х1 (жылдар), мамандықты жұмыс істеген жылдар мерзімі х2(жыл), өнім өндіру х3 (жұмысшыға дана есебінде бір ауысым ішіндегі) деректері бар.
|
Бақылаудың нөмірі
|
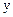 - жалақы - жалақы
|
 - жас шамасы - жас шамасы
| 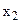 -мамандық бойынша жұмыс мерзімі -мамандық бойынша жұмыс мерзімі
|
х3 - өнім өндіру
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
Жалақы бойынша жиынтық регрессиялық моделі жасалған:  . .
Факторлар арасындағы мультиколлинеарлықтын бар болуын тексеріп және, егер мультиколлинеарлық бар болса, оны жою керек.
Шешуі. Ең алдымен қосақты корреляция коэффициенттерін табамыз. Соңғы жолда сәйкес бағана бойынша соммасының көрсеткіші болатындай етіп, кесте құрамыз:
| | 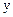
| 
| 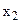
| 
| 
| 
| 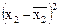
| 
| | |
|
|
|
|
| 44,22
| 63,20
| 4,41
| | |
|
|
|
|
| 18,92
| 25,50
| 34,81
| | |
|
|
|
|
| 0,12
| 15,60
| 16,81
| | |
|
|
|
|
| 13,32
| 15,60
| 4,41
| | |
|
|
|
|
| 160,02
| 119,90
| 16,81
| | |
|
|
|
|
| 87,42
| 36,60
| 1,21
| | |
|
|
|
|
| 5,52
| 9,30
| 4,41
| | |
|
|
|
|
| 18,92
| 81,90
| 34,81
| | |
|
|
|
|
| 205,92
| 290,70
| 0,01
| | |
|
|
|
|
| 128,82
| 122,10
| 15,21
| | |
|
|
|
|
| 58,52
| 48,30
| 16,81
| | |
|
|
|
|
| 31,92
| 48,30
| 1,21
| | |
|
|
|
|
| 113,42
| 63,20
| 9,61
| | |
|
|
|
|
| 152,52
| 36,60
| 15,21
| | |
|
|
|
|
| 31,92
| 80,10
| 1,21
| | |
|
|
|
|
| 18,92
| 1,10
| 1,21
| | |
|
|
|
|
| 18,92
| 36,60
| 34,81
| | |
|
|
|
|
| 5,52
| 36,60
| 15,21
| | |
|
|
|
|
| 44,22
| 15,60
| 1,21
| | |
|
|
|
|
| 113,42
| 80,10
| 4,41
| 
|
|
|
|
|
| 1272,55
| 1226,95
| 233,8
| | | | | | | | | | |
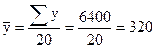 , ,  , ,
 , , 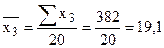
Енді орташа квадраттық ауытқуларды табамыз:
 , ,  , ,
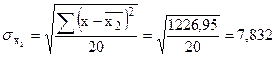 , , 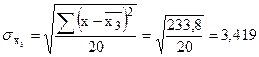
Кейін айнымалылар көбейтіндісіне орташа мәндерін табамыз:
Онда
 , ,  , ,  , ,  , ,
 , , 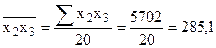
Енді корреляцияның қосақты коэффициенттерін табуға болады:
 , ,  , ,
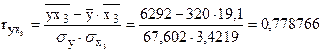 , ,
 , ,
 , ,
 . .
Корреляциялық матрицаны құрамыз:
|
| 
| 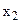
| 
| 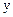
| 
|
| 0,935263
| 0,615448
| 0,853056
| 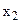
| 0,935263
|
| 0,69661
| 0,849877
| 
| 0,615448
| 0,69661
|
| 0,778766
| 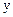
| 0,853056
| 0,849877
| 0,778766
|
|
Факторларды мультиколлинеарлыққа тексереміз. Мультиколлинеарлық тәуелділігі бар болады, егер қос корреляция коэффициенті  болса. болса.
Мұнда  және және 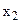 факторлар үшін осы шарт орындалады. факторлар үшін осы шарт орындалады.
Осылайша,  және және 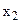 факторлары арасында сызықтық тәуелділік бар. Мультиколлинеарлықты жою үшін айнымалыларды шығару әдісін қолданамыз. Ең кіші факторлары арасында сызықтық тәуелділік бар. Мультиколлинеарлықты жою үшін айнымалыларды шығару әдісін қолданамыз. Ең кіші  мәніне ие фактордан құтыламыз. Ал мәніне ие фактордан құтыламыз. Ал  , (0,853056>0,849877) болғандықтан , (0,853056>0,849877) болғандықтан 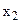 факторынан құтылған жөн. Мультиколлинеарлық түсіндірмелі, себебі жұмыс істеген жылдар көлемі жұмыскердің жасына тәуелді. факторынан құтылған жөн. Мультиколлинеарлық түсіндірмелі, себебі жұмыс істеген жылдар көлемі жұмыскердің жасына тәуелді. 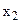 факторды шығарып, регрессия теңдеуін құрамыз (6-7тақырыптарды қараңыз). факторды шығарып, регрессия теңдеуін құрамыз (6-7тақырыптарды қараңыз).
Ол теңдеу мынадай болады:  . .

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Пункты решения командира взвода на организацию боя. уяснение полученной задачи; оценка обстановки; принятие решения; проведение рекогносцировки; отдача боевого приказа; организация взаимодействия...
Что такое пропорции?
Это соотношение частей целого между собой. Что может являться частями в образе или в луке...
Растягивание костей и хрящей. Данные способы применимы в случае закрытых зон роста.
Врачи-хирурги выяснили...
|
Деятельность сестер милосердия общин Красного Креста ярко проявилась в период Тритоны – интервалы, в которых содержится три тона. К тритонам относятся увеличенная кварта (ув.4) и уменьшенная квинта (ум.5). Их можно построить на ступенях натурального и гармонического мажора и минора.
...
Понятие о синдроме нарушения бронхиальной проходимости и его клинические проявления Синдром нарушения бронхиальной проходимости (бронхообструктивный синдром) – это патологическое состояние...
Опухоли яичников в детском и подростковом возрасте Опухоли яичников занимают первое место в структуре опухолей половой системы у девочек и встречаются в возрасте 10 – 16 лет и в период полового созревания...
|
|

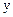 - жалақы
- жалақы
 - жас шамасы
- жас шамасы
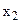 -мамандық бойынша жұмыс мерзімі
-мамандық бойынша жұмыс мерзімі
 .
.


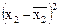


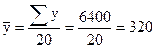 ,
,  ,
, ,
, 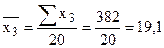
 ,
,  ,
,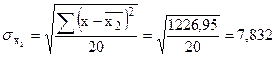 ,
, 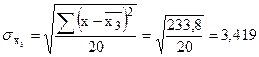





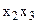
 ,
,  ,
,  ,
,  ,
, ,
, 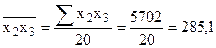
 ,
,  ,
,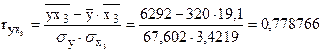 ,
, ,
, ,
, .
.

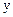
 болса.
болса. мәніне ие фактордан құтыламыз. Ал
мәніне ие фактордан құтыламыз. Ал  , (0,853056>0,849877) болғандықтан
, (0,853056>0,849877) болғандықтан  .
.


