Тақырып. Сызықты емес регрессия және корреляция.
Мысал. Әр түрлі шаруашылықтармен берілген тыңайтқыштар мен осы жағдайда алынған өнім көлемі белгілі болсын. Кестеде Х – тыңайтқыш (удобрение) мөлшері (кг/га) және У - өнімділік (урожайность) (ц/га) берілген.
Регрессия сызықтарының теңдеулерін құрыңыз: а) Екі дәрежелі параболаны; б) Тең бүйірлі гиперболаны. Корреляция индексі бойынша Х және У факторлары арасындағы тығыздықты бағалаңыз. Шешуі. а) Екінші ретті параболаның регрессия теңдеуін келесі түрде іздейміз: Параболаның регрессия теңдеуінің коэффициенттерін табу үшін нормалдық (қалыпты)теңдеулер жүйесі мынадай болады:
Есептеуші кесте құрамыз:
Нәтижесінде нормалдық теңдеулер жүйесі мына түрде болады:
Крамер әдісін қолданып, теңдеулер жүйесін шешеміз:
Онда
Регрессия теңдеуінін келесі түрін аламыз: Х және У факторлар арасындағы тығыздық қатынасын табу үшінкорреляция индексі R – ді табамыз.
Корреляция индексін анықтау үшін, есептеуші кестені құрамыз:
Мұндағы
Корреляция индексін келесі формула бойынша анықтаймыз:
Корреляция индексі R=0,8238 тең болды, бұдан мына қорытындыны шығаруға болады: х және у арасындағы байланыс тығыз.
б) Тең бүйірлі гиперболаның регрессия теңдеуін келесі түрде іздейміз:
Тең бүйірлі гиперболаның регрессия теңдеуінің коэффициенттерін табу үшін, келесі нормалдық теңдеулер жүйесін аламыз:
Есептеуші кестені құрамыз:
Біздің жағдайда келесі жұйені аламыз:
Крамер әдісін пайдаланып, теңдеулер жүйесін шешеміз:
Онда Келесі регрессия теңдеуі шығады: Корреляция индексі жоғарыдағы (а-пунктіндегі)- дей анықталады. Есептеуші кестені құрамыз:
Енді корреляция индексін табамыз: Сонымен, негізгі мәліметтер параболалық функциямен жеткілікті жақсы жуықталады, ал гиперболамен өте жаман сипатталады.
|

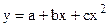 .
.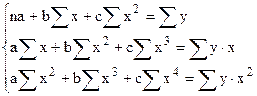

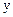


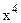



 ,
, 
 ,
, 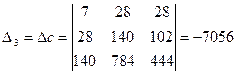
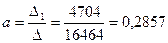 ,
, 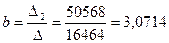 ,
, 
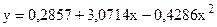


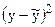


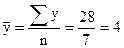
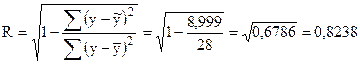

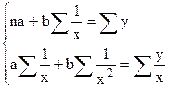
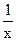



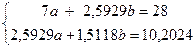
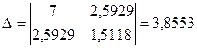 ,
, 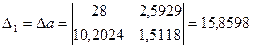

 ,
, 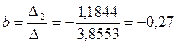 .
. .
. , бұдан мына қорытынды шығарамыз: х және у арасындағы байланыс әлсіз немесе байланыс жоқ; деп те айтуға болады.
, бұдан мына қорытынды шығарамыз: х және у арасындағы байланыс әлсіз немесе байланыс жоқ; деп те айтуға болады.


