З бетінше орындауға арналған есептер. 1. Бір бөлмелі пәтердің баға жөнінде және бір аймақтағы 10 келісім бойынша оның жалпы ауданы
1. Бір бөлмелі пәтердің баға жөнінде және бір аймақтағы 10 келісім бойынша оның жалпы ауданы жөнінде деректер бар:
| Пәтердің бағасы (млн.доллар)
|
|
|
|
|
|
|
|
|
|
| | Аудан, м2
|
|
|
|
|
|
|
|
|
|
|
 сызықты регрессия параметрлері есептелген және көрсеткіштер арасындағы байланыс тығыздығы сызықты регрессия параметрлері есептелген және көрсеткіштер арасындағы байланыс тығыздығы  белгілі. белгілі.
Теңдеудің жалпы статистикалық маңыздылығын және сонымен қатар регрессия мен корреляция параметрлерін 0,05 маңыздылығы кезінде Фишер және Стьюдент критериілер арқылы бағалаңыз.
2. Қазақстанның 20 аймағы бойынша жандық орта жылдық кіріс теңдеуінің ауыр еңбекпен шұғылданатын адамдар, жалпы жұмыс істейтін (х1), белсенді тұрғындар, барлық тұрғындардың саны (х2) мәндерін Ғ-Фишер критериі арқылы статистикалық маңыздылығын бағалаңыз, егер корреляция коэффициенті  болса. Жиынтық регрессия теңдеуінің болса. Жиынтық регрессия теңдеуінің   және және  айнымалалары кезінде коэффициенттерінің маңыздылығын айнымалалары кезінде коэффициенттерінің маңыздылығын  -Стьюдент критериі арқылы есептеңіз. Қосалқы корреляция коэффициенттері келесі мәндерде болады: -Стьюдент критериі арқылы есептеңіз. Қосалқы корреляция коэффициенттері келесі мәндерде болады: 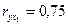 , ,  , ,  . .
12 тақырып. Гетероскедастикалық;
Мысал. 20 зерттеу бойынша азық-түлікке у (бірлік ақша) моделі құрылған у=20,84+0,44 х-тың әр мәнінде қалдықтар шамалары  мынадай болады: мынадай болады:
| №
| 
| Қалдық

| |
|
| -12,0
| |
|
| -11,7
| |
|
| -5,4
| |
|
| -5,6
| |
|
| -2,8
| |
|
| 0,8
| |
|
| -1,6
| |
|
| -4,0
| |
|
| -6,2
| |
|
| 6,6
| |
|
| 13,7
| |
|
| 12,2
| |
|
| 4,4
| |
|
| 4,0
| |
|
| 3,4
| |
|
| 23,2
| |
|
| 16,2
| |
|
| -16,8
| |
|
| -27,8
| |
|
| 9,8
|
1. Х айнымалының мәніне байланысты қалдықтар графигін салыңыз және шешімдер жасаңыз.
2. Гетероскедастиканы анықтау үшін Гольдфельд – Квандт тестін қолданыңыз.
3. Жалпыланған ең кіші квадраттар әдісін пайдаланып, модельді жақсартыңыз.
Шешуі. Қалдықтар графигі мынадай болады:
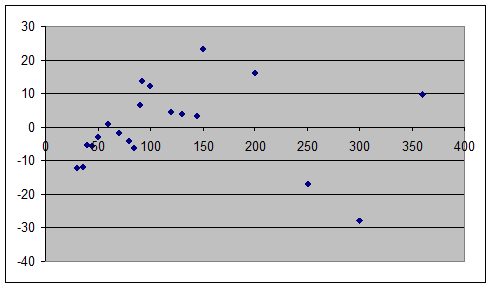
Әртүрлі х-тің мәндерінде қалдықтар тербелесі бірдей еместігін графигі көрсетеді: егер х<90 болса, онда e>0; ал егер х  (90;200) аралықта жатса, онда e>0. Егер х>200 үлкен болса, е-нің өзгеру аралығы, х-тің кіші мәндеріне қарағанда, одан да көп. Сонымен, график арқылы қалдықтардың гетероскедастикалықтың барын болжауға болады. (90;200) аралықта жатса, онда e>0. Егер х>200 үлкен болса, е-нің өзгеру аралығы, х-тің кіші мәндеріне қарағанда, одан да көп. Сонымен, график арқылы қалдықтардың гетероскедастикалықтың барын болжауға болады.
3. Гольдфельд-Квандт тестін қолдану үшін у жөнінде ақпараттар қажет. Бұл ақпараттар берілмесе де, оларды табуға болады. Регрессия теңдеуі негізінде  есептеуші мәндерін табамыз. Енді есептеуші мәндерін табамыз. Енді  фактілік мәндерін табамыз. фактілік мәндерін табамыз.

| 
| e
| 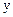
| |
|
| -12,0
|
| |
| 36,7
| -11,7
|
| |
| 38,4
| -5,4
|
| |
| 40,6
| -5,6
|
| |
| 42,8
| -2,8
|
| |
| 47,2
| 0,8
|
| |
| 51,6
| -1,6
|
| |
|
| -4,0
|
| |
| 58,2
| -6,2
|
| |
| 60,4
| 6,6
|
| |
| 61,3
| 13,7
|
| |
| 64,8
| 12,2
|
| |
| 73,6
| 4,4
|
| |
|
| 4,0
|
| |
| 84,6
| 3,4
|
| |
| 86,8
| 23,2
|
| |
| 108,8
| 16,2
|
| |
| 130,8
| -16,8
|
| |
| 152,8
| -27,8
|
| |
| 179,2
| 9,8
|
|
Орталық С бақылауларды кестеден шығарайық.. Жиынтықты екі бөлікке бөлеміз: а) бір бөлігінде х мәндері орта мәндерінен төмен; б) екінші бөлігінде – х мәндері орта мәндерінен жоғары. С=4 болсын, бұл бақылаулар мынадай реттік нөмірлерімен: 9,10,11,12. Онда әр бөлікте 8 бақылаулардан қалады. Әр бөліктін регрессия теңдеуін табамыз. Бірінші бөлігін қарастырамыз және оған есептеуші кестені құрамыз.
| №
| 
| 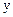
| 
| 
| 
| 
| 
| |
|
|
|
| -21,375
| 456,8906
| -16,125
| 260,0156
| |
|
|
|
| -15,375
| 236,3906
| -13,125
| 172,2656
| |
|
|
|
| -11,375
| 129,3906
| -5,125
| 26,26563
| |
|
|
|
| -6,375
| 40,64063
| -3,125
| 9,765625
| |
|
|
|
| -1,375
| 1,890625
| 1,875
| 3,515625
| |
|
|
|
| 8,625
| 74,39063
| 9,875
| 97,51563
| |
|
|
|
| 18,625
| 346,8906
| 11,875
| 141,0156
| |
|
|
|
| 28,625
| 819,3906
| 13,875
| 192,5156
| | Σ
|
|
|
|
| 2105,875
|
| 902,875
|
Қажетті мәндерін табамыз:
 , ,  , ,  , ,
 , ,  , ,
Онда
 , , 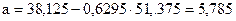
Сонда, мынадай теңдеуді аламыз 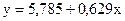
Ұқсас екінші бөлігіне кесте құрамыз:
| №
| 
| 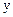
| 
| 
| 
| 
| 
| |
|
|
|
| -86,875
| 7547,266
| -35,875
| 1287,016
| |
|
|
|
| -76,875
| 5909,766
| -31,875
| 1016,016
| |
|
|
|
| -61,875
| 3828,516
| -25,875
| 669,5156
| |
|
|
|
| -56,875
| 3234,766
| -3,875
| 15,01563
| |
|
|
|
| -6,875
| 47,26563
| 11,125
| 123,7656
| |
|
|
|
| 43,125
| 1859,766
| 0,125
| 0,015625
| |
|
|
|
| 93,125
| 8672,266
| 11,125
| 123,7656
| |
|
|
|
| 153,125
| 23447,27
| 75,125
| 5643,766
| | Σ
|
|
|
|
| 54546,88
|
| 8878,875
|
Қажетті мәндерін табамыз:
 , , 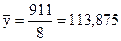 , ,  , ,
 , , 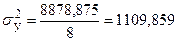 , ,
Онда
 , , 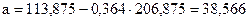 . .
Сонда, мынадай теңдеуді аламыз  . .
Енді әр топқа: у-тін теоретикалық мәндерін, қалдықтар е-ні және оның квадраттарын е2 анықтаймыз.

| 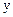
|  топ арқылы
топ арқылы
| етоп арқылы
| е2топ арқылы
| |
|
| 24,66967
| -2,66967
| 7,12716
| |
|
| 28,44661
| -3,44661
| 11,8791
| |
|
| 30,96456
| 2,035437
| 4,143002
| |
|
| 34,11201
| 0,887992
| 0,78853
| |
|
| 37,25945
| 2,740547
| 7,510599
| |
|
| 43,55434
| 4,445658
| 19,76387
| |
|
| 49,84923
| 0,150769
| 0,022731
| |
|
| 56,14412
| -4,14412
| 17,17374
| |
|
|
|
| Σ=68,40874
|
Ұқсас

| 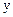
|  топ арқылы топ арқылы
| етоп арқылы
| е2топ
арқылы
| |
|
| 82,24961
| -4,24961
| 18,05921
| |
|
| 85,88995
| -3,88995
| 15,13168
| |
|
| 91,35044
| -3,35044
| 11,22547
| |
|
| 93,17061
| 16,82939
| 283,2284
| |
|
| 111,3723
| 13,62773
| 185,715
| |
|
| 129,5739
| -15,5739
| 242,5474
| |
|
| 147,7756
| -22,7756
| 518,7277
| |
|
| 169,6176
| 19,38241
| 375,6779
| |
|
|
|
| Σ=1650,313
|
Енді қалдықтар квадраттарының ең үлкен соммасының кіші соммасына қатынасын табамыз: 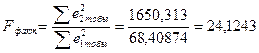
5% маңыздылық деңгейінде және дәреже еркіндік санында 8-2=6 (өйткені әр топта 8 элементтен бар) осы шаманы (Ғ фактолықты) Ғ-критериінің кестелік мәнімен салыстырамыз:  . Сонымен Ғфакт>Ғкриз, бұдан мына қорытындыға келеміз: қалдықтардың гетероскедастикалығы бар. Қалдықтардың гетероскедастикалығын төмендету үшін жалпылаған ең кіші квадраттар әдісін қолдануға болады. Ол үшін есептеуші кесте құрамыз. . Сонымен Ғфакт>Ғкриз, бұдан мына қорытындыға келеміз: қалдықтардың гетероскедастикалығы бар. Қалдықтардың гетероскедастикалығын төмендету үшін жалпылаған ең кіші квадраттар әдісін қолдануға болады. Ол үшін есептеуші кесте құрамыз.
| №
| x
| y
| y/x
| 1/x
| |
|
|
| 0,733333
| 0,033333
| |
|
|
| 0,694444
| 0,027778
| |
|
|
| 0,825
| 0,025
| |
|
|
| 0,777778
| 0,022222
| |
|
|
| 0,8
| 0,02
| |
|
|
| 0,8
| 0,016667
| |
|
|
| 0,714286
| 0,014286
| |
|
|
| 0,65
| 0,0125
| |
|
|
| 0,611765
| 0,011765
| |
|
|
| 0,744444
| 0,011111
| |
|
|
| 0,815217
| 0,01087
| |
|
|
| 0,77
| 0,01
| |
|
|
| 0,65
| 0,008333
| |
|
|
| 0,630769
| 0,007692
| |
|
|
| 0,606897
| 0,006897
| |
|
|
| 0,733333
| 0,006667
| |
|
|
| 0,625
| 0,005
| |
|
|
| 0,456
| 0,004
| |
|
|
| 0,416667
| 0,003333
| |
|
|
| 0,525
| 0,002778
| | Σ
|
|
| 13,57993
| 0,260231
|
Нормалдық теңдеулер жүйесі мынадай болады:

Онда болады:
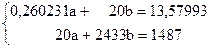
Теңдеулер жүйесін Крамер әдісімен шығарыңыз. Онда болады:
 , , 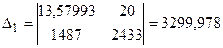
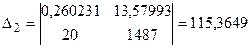
Онда  , ,  . .
Осыдан шыққан теңдеуінде  гетероскедастикалылық жойылған. гетероскедастикалылық жойылған.

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Основные структурные физиотерапевтические подразделения Физиотерапевтическое подразделение является одним из структурных подразделений лечебно-профилактического учреждения, которое предназначено для оказания физиотерапевтической помощи...
Почему важны муниципальные выборы? Туристическая фирма оставляет за собой право, в случае причин непреодолимого характера, вносить некоторые изменения в программу тура без уменьшения общего объема и качества услуг, в том числе предоставлять замену отеля на равнозначный...
Тема 2: Анатомо-топографическое строение полостей зубов верхней и нижней челюстей. Полость зуба — это сложная система разветвлений, имеющая разнообразную конфигурацию...
|
Разновидности сальников для насосов и правильный уход за ними
Сальники, используемые в насосном оборудовании, служат для герметизации пространства образованного кожухом и рабочим валом, выходящим через корпус наружу...
Дренирование желчных протоков Показаниями к дренированию желчных протоков являются декомпрессия на фоне внутрипротоковой гипертензии, интраоперационная холангиография, контроль за динамикой восстановления пассажа желчи в 12-перстную кишку...
Деятельность сестер милосердия общин Красного Креста ярко проявилась в период Тритоны – интервалы, в которых содержится три тона. К тритонам относятся увеличенная кварта (ув.4) и уменьшенная квинта (ум.5). Их можно построить на ступенях натурального и гармонического мажора и минора.
...
|
|

 сызықты регрессия параметрлері есептелген және көрсеткіштер арасындағы байланыс тығыздығы
сызықты регрессия параметрлері есептелген және көрсеткіштер арасындағы байланыс тығыздығы  белгілі.
белгілі. болса. Жиынтық регрессия теңдеуінің
болса. Жиынтық регрессия теңдеуінің 
 және
және  айнымалалары кезінде коэффициенттерінің маңыздылығын
айнымалалары кезінде коэффициенттерінің маңыздылығын  -Стьюдент критериі арқылы есептеңіз. Қосалқы корреляция коэффициенттері келесі мәндерде болады:
-Стьюдент критериі арқылы есептеңіз. Қосалқы корреляция коэффициенттері келесі мәндерде болады: 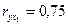 ,
,  ,
,  .
. мынадай болады:
мынадай болады:


 (90;200) аралықта жатса, онда e>0. Егер х>200 үлкен болса, е-нің өзгеру аралығы, х-тің кіші мәндеріне қарағанда, одан да көп. Сонымен, график арқылы қалдықтардың гетероскедастикалықтың барын болжауға болады.
(90;200) аралықта жатса, онда e>0. Егер х>200 үлкен болса, е-нің өзгеру аралығы, х-тің кіші мәндеріне қарағанда, одан да көп. Сонымен, график арқылы қалдықтардың гетероскедастикалықтың барын болжауға болады. есептеуші мәндерін табамыз. Енді
есептеуші мәндерін табамыз. Енді  фактілік мәндерін табамыз.
фактілік мәндерін табамыз.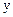





 ,
,  ,
,  ,
, ,
,  ,
, ,
, 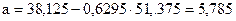
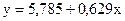

 ,
, 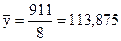 ,
,  ,
, ,
, 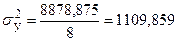 ,
, ,
, 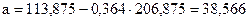 .
. .
. топ арқылы
топ арқылы
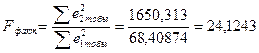
 . Сонымен Ғфакт>Ғкриз, бұдан мына қорытындыға келеміз: қалдықтардың гетероскедастикалығы бар. Қалдықтардың гетероскедастикалығын төмендету үшін жалпылаған ең кіші квадраттар әдісін қолдануға болады. Ол үшін есептеуші кесте құрамыз.
. Сонымен Ғфакт>Ғкриз, бұдан мына қорытындыға келеміз: қалдықтардың гетероскедастикалығы бар. Қалдықтардың гетероскедастикалығын төмендету үшін жалпылаған ең кіші квадраттар әдісін қолдануға болады. Ол үшін есептеуші кесте құрамыз.
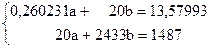
 ,
, 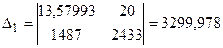
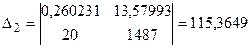
 ,
,  .
. гетероскедастикалылық жойылған.
гетероскедастикалылық жойылған.


