З бетінше орындауға арналған есептер.
1.
3. Жалпыланған ең кіші квадраттар әдісінің нәтижелерін пайдаланып, бастапқы регрессия теңдеуінің коэффиценттерін бағалаңыз.
Тақырып. Бір уақытты теңдеулер жүйесі.
Мысал. Қандай бір ел үшін у жыинтық кірісі, түтыну көлемі С және инвестициялар I 10 жыл бойынша (ш. бірл.) алынған мәліметтері бар.
Кейнстің кірісті қалыптастыру моделін қолданып, түтыну фунуциясын салу қажет:
Шешуі. Кәдімгі ең кіші квадраттар әдісімен түтыну функциясының теңдеулер параметрлерін бағалайық. Жұптық сызықтық регрессия үшін нормалдық (қалыпты) теңдеулер жүйесін құрайық:
Есептеуші кестеде қосындылар мәндері көрсетілген:
Сонымен, ең кіші квадраттар әдісінің нормалдық (қалыпты) теңдеулер жүйесі келесі турде болады:
Бұл жүйені Крамер әдісімен шешіп a және b коэффициенттерін табамыз:
Онда Тұтыну функциясының құрылымдық теңдеуін кәдімгі ең кіші квадраттар (ЕКК) әдісімен тікелеу бағалау осындай нәтижелерге әкеледі:
Бұл жағдайда a және b коэффициенттердін бағалары ығысқан және ауқатты емес, өйткені тәуелді айнымалы Сондықтан, біз ең кіші жанама квадраттар (ЕКЖК) әдісін қолданып, модельдін құрылымдық коэффициенттерінің бағаларын табайық. Ең алдымен берілген
Келесі нормалдық (қалыпты) теңдеулер жүйесін аламыз:
Жүйені Крамер әдісімен шешеміз:
Онда Түтыну фунуциянын құрылымдық коэффициенттерінің мәндерін келесі формулалар бойынша есептейік:
Ең кіші жанама квадраттар (ЕКЖК) әдісімен табылған құрылымдық коэффициенттерінің бағалары жылжымаған және ауқатты болады. Сонымен, Кейнс моделіндегі түтыну функциясы мына түрде болады:
|

 моделі құрылған. Дарбин-Уотсон критериін есептеңіз және 5% мәнділік кезінде нәтижені бағалаңыз, егер жоғары шекара
моделі құрылған. Дарбин-Уотсон критериін есептеңіз және 5% мәнділік кезінде нәтижені бағалаңыз, егер жоғары шекара  және төменгі шекара
және төменгі шекара  болса және
болса және 



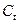



 ,
, 
 ..
.. ,
, 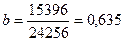 .
.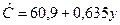 .
.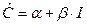 теңдеудің коэффициенттерін анықтаймыз, оны кәдімгі (ЕККӘ)-ны қолдана отырып табамыз. Есептеуші кестені құрамыз:
теңдеудің коэффициенттерін анықтаймыз, оны кәдімгі (ЕККӘ)-ны қолдана отырып табамыз. Есептеуші кестені құрамыз: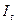


 немесе
немесе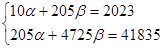
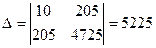 ,
, 
 .
. ,
,  және модель келтірілген түрде мынадай болады
және модель келтірілген түрде мынадай болады  .
. ,
,  .
.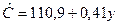 . Құрылымдық коэффициент b түтынуға шектік бейімділікті сипаттайды, яғни егер жиін кірісі 1шарт.бір. өссе, онда түтыну көлемінің 0,41 шарт.бірл. өсүін күтуге болады.
. Құрылымдық коэффициент b түтынуға шектік бейімділікті сипаттайды, яғни егер жиін кірісі 1шарт.бір. өссе, онда түтыну көлемінің 0,41 шарт.бірл. өсүін күтуге болады.


